Table of Contents

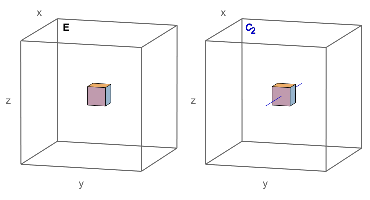
Orientation X

Symmetry Operations

In the C2 Point Group, with orientation X there are the following symmetry operations

Operator Orientation
$\text{E}$ $\{0,0,0\}$ ,
$C_2$ $\{1,0,0\}$ ,

Different Settings

Character Table

$ $ $ \text{E} \,{\text{(1)}} $ $ C_2 \,{\text{(1)}} $
$ \text{A} $ $ 1 $ $ 1 $
$ \text{B} $ $ 1 $ $ -1 $

Product Table

$ $ $ \text{A} $ $ \text{B} $
$ \text{A} $ $ \text{A} $ $ \text{B} $
$ \text{B} $ $ \text{B} $ $ \text{A} $

Sub Groups with compatible settings

Super Groups with compatible settings

Invariant Potential expanded on renormalized spherical Harmonics

Any potential (function) can be written as a sum over spherical harmonics. $$V(r,\theta,\phi) = \sum_{k=0}^{\infty} \sum_{m=-k}^{k} A_{k,m}(r) C^{(m)}_k(\theta,\phi)$$ Here $A_{k,m}(r)$ is a radial function and $C^{(m)}_k(\theta,\phi)$ a renormalised spherical harmonics. $$C^{(m)}_k(\theta,\phi)=\sqrt{\frac{4\pi}{2k+1}}Y^{(m)}_k(\theta,\phi)$$ The presence of symmetry induces relations between the expansion coefficients such that $V(r,\theta,\phi)$ is invariant under all symmetry operations. For the C2 Point group with orientation X the form of the expansion coefficients is:

Expansion

$$A_{k,m} = \begin{cases} A(0,0) & k=0\land m=0 \\ -A(1,1) & k=1\land m=-1 \\ A(1,1) & k=1\land m=1 \\ A(2,2) & k=2\land (m=-2\lor m=2) \\ i B(2,1) & k=2\land (m=-1\lor m=1) \\ A(2,0) & k=2\land m=0 \\ -A(3,3) & k=3\land m=-3 \\ -i B(3,2) & k=3\land m=-2 \\ -A(3,1) & k=3\land m=-1 \\ A(3,1) & k=3\land m=1 \\ i B(3,2) & k=3\land m=2 \\ A(3,3) & k=3\land m=3 \\ A(4,4) & k=4\land (m=-4\lor m=4) \\ i B(4,3) & k=4\land (m=-3\lor m=3) \\ A(4,2) & k=4\land (m=-2\lor m=2) \\ i B(4,1) & k=4\land (m=-1\lor m=1) \\ A(4,0) & k=4\land m=0 \\ -A(5,5) & k=5\land m=-5 \\ -i B(5,4) & k=5\land m=-4 \\ -A(5,3) & k=5\land m=-3 \\ -i B(5,2) & k=5\land m=-2 \\ -A(5,1) & k=5\land m=-1 \\ A(5,1) & k=5\land m=1 \\ i B(5,2) & k=5\land m=2 \\ A(5,3) & k=5\land m=3 \\ i B(5,4) & k=5\land m=4 \\ A(5,5) & k=5\land m=5 \\ A(6,6) & k=6\land (m=-6\lor m=6) \\ i B(6,5) & k=6\land (m=-5\lor m=5) \\ A(6,4) & k=6\land (m=-4\lor m=4) \\ i B(6,3) & k=6\land (m=-3\lor m=3) \\ A(6,2) & k=6\land (m=-2\lor m=2) \\ i B(6,1) & k=6\land (m=-1\lor m=1) \\ A(6,0) & k=6\land m=0 \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{A[0, 0], k == 0 && m == 0}, {-A[1, 1], k == 1 && m == -1}, {A[1, 1], k == 1 && m == 1}, {A[2, 2], k == 2 && (m == -2 || m == 2)}, {I*B[2, 1], k == 2 && (m == -1 || m == 1)}, {A[2, 0], k == 2 && m == 0}, {-A[3, 3], k == 3 && m == -3}, {(-I)*B[3, 2], k == 3 && m == -2}, {-A[3, 1], k == 3 && m == -1}, {A[3, 1], k == 3 && m == 1}, {I*B[3, 2], k == 3 && m == 2}, {A[3, 3], k == 3 && m == 3}, {A[4, 4], k == 4 && (m == -4 || m == 4)}, {I*B[4, 3], k == 4 && (m == -3 || m == 3)}, {A[4, 2], k == 4 && (m == -2 || m == 2)}, {I*B[4, 1], k == 4 && (m == -1 || m == 1)}, {A[4, 0], k == 4 && m == 0}, {-A[5, 5], k == 5 && m == -5}, {(-I)*B[5, 4], k == 5 && m == -4}, {-A[5, 3], k == 5 && m == -3}, {(-I)*B[5, 2], k == 5 && m == -2}, {-A[5, 1], k == 5 && m == -1}, {A[5, 1], k == 5 && m == 1}, {I*B[5, 2], k == 5 && m == 2}, {A[5, 3], k == 5 && m == 3}, {I*B[5, 4], k == 5 && m == 4}, {A[5, 5], k == 5 && m == 5}, {A[6, 6], k == 6 && (m == -6 || m == 6)}, {I*B[6, 5], k == 6 && (m == -5 || m == 5)}, {A[6, 4], k == 6 && (m == -4 || m == 4)}, {I*B[6, 3], k == 6 && (m == -3 || m == 3)}, {A[6, 2], k == 6 && (m == -2 || m == 2)}, {I*B[6, 1], k == 6 && (m == -1 || m == 1)}, {A[6, 0], k == 6 && m == 0}}, 0]

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{0, 0, A(0,0)} , 
       {1,-1, (-1)*(A(1,1))} , 
       {1, 1, A(1,1)} , 
       {2, 0, A(2,0)} , 
       {2,-1, (I)*(B(2,1))} , 
       {2, 1, (I)*(B(2,1))} , 
       {2,-2, A(2,2)} , 
       {2, 2, A(2,2)} , 
       {3,-1, (-1)*(A(3,1))} , 
       {3, 1, A(3,1)} , 
       {3,-2, (-I)*(B(3,2))} , 
       {3, 2, (I)*(B(3,2))} , 
       {3,-3, (-1)*(A(3,3))} , 
       {3, 3, A(3,3)} , 
       {4, 0, A(4,0)} , 
       {4,-1, (I)*(B(4,1))} , 
       {4, 1, (I)*(B(4,1))} , 
       {4,-2, A(4,2)} , 
       {4, 2, A(4,2)} , 
       {4,-3, (I)*(B(4,3))} , 
       {4, 3, (I)*(B(4,3))} , 
       {4,-4, A(4,4)} , 
       {4, 4, A(4,4)} , 
       {5,-1, (-1)*(A(5,1))} , 
       {5, 1, A(5,1)} , 
       {5,-2, (-I)*(B(5,2))} , 
       {5, 2, (I)*(B(5,2))} , 
       {5,-3, (-1)*(A(5,3))} , 
       {5, 3, A(5,3)} , 
       {5,-4, (-I)*(B(5,4))} , 
       {5, 4, (I)*(B(5,4))} , 
       {5,-5, (-1)*(A(5,5))} , 
       {5, 5, A(5,5)} , 
       {6, 0, A(6,0)} , 
       {6,-1, (I)*(B(6,1))} , 
       {6, 1, (I)*(B(6,1))} , 
       {6,-2, A(6,2)} , 
       {6, 2, A(6,2)} , 
       {6,-3, (I)*(B(6,3))} , 
       {6, 3, (I)*(B(6,3))} , 
       {6,-4, A(6,4)} , 
       {6, 4, A(6,4)} , 
       {6,-5, (I)*(B(6,5))} , 
       {6, 5, (I)*(B(6,5))} , 
       {6,-6, A(6,6)} , 
       {6, 6, A(6,6)} }

One particle coupling on a basis of spherical harmonics

The operator representing the potential in second quantisation is given as: $$ O = \sum_{n'',l'',m'',n',l',m'} \left\langle \psi_{n'',l'',m''}(r,\theta,\phi) \left| V(r,\theta,\phi) \right| \psi_{n',l',m'}(r,\theta,\phi) \right\rangle a^{\dagger}_{n'',l'',m''}a^{\phantom{\dagger}}_{n',l',m'}$$ For the quantisation of the wave-function (physical meaning of the indices n,l,m) we can choose a basis of spherical harmonics times some radial function, i.e. $\psi_{n,l,m}(r,\theta,\phi)=R_{n,l}(r)Y_{m}^{(l)}(\theta,\phi)$. With this choice the integral for the expectation value in front of the creation and annihilation operators separates into a radial part and angular part. The angular part has an analytical solution, the radial integral is cast int a parameter. $$ A_{n''l'',n'l'}(k,m) = \left\langle R_{n'',l''} \left| A_{k,m}(r) \right| R_{n',l'} \right\rangle $$ Note the difference between the function $A_{k,m}$ and the parameter $A_{n''l'',n'l'}(k,m)$

we can express the operator as $$ O = \sum_{n'',l'',m'',n',l',m',k,m} A_{n''l'',n'l'}(k,m) \left\langle Y_{l''}^{(m'')}(\theta,\phi) \left| C_{k}^{(m)}(\theta,\phi) \right| Y_{l'}^{(m')}(\theta,\phi) \right\rangle a^{\dagger}_{n'',l'',m''}a^{\phantom{\dagger}}_{n',l',m'}$$

The table below shows the expectation value of $O$ on a basis of spherical harmonics. We suppressed the principle quantum number indices. Note that in principle $A_{l'',l'}(k,m)$ can be complex. Instead of allowing complex parameters we took $A_{l'',l'}(k,m) + \mathrm{I}\, B_{l'',l'}(k,m)$ (with both A and B real) as the expansion parameter.

$ $ $ {Y_{0}^{(0)}} $ $ {Y_{-1}^{(1)}} $ $ {Y_{0}^{(1)}} $ $ {Y_{1}^{(1)}} $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ {Y_{0}^{(0)}} $$ \text{Ass}(0,0) $$\color{darkred}{ -\frac{\text{Asp}(1,1)}{\sqrt{3}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{\text{Asp}(1,1)}{\sqrt{3}} }$$ \frac{\text{Asd}(2,2)}{\sqrt{5}} $$ -\frac{i \text{Bsd}(2,1)}{\sqrt{5}} $$ \frac{\text{Asd}(2,0)}{\sqrt{5}} $$ -\frac{i \text{Bsd}(2,1)}{\sqrt{5}} $$ \frac{\text{Asd}(2,2)}{\sqrt{5}} $$\color{darkred}{ -\frac{\text{Asf}(3,3)}{\sqrt{7}} }$$\color{darkred}{ \frac{i \text{Bsf}(3,2)}{\sqrt{7}} }$$\color{darkred}{ -\frac{\text{Asf}(3,1)}{\sqrt{7}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{\text{Asf}(3,1)}{\sqrt{7}} }$$\color{darkred}{ -\frac{i \text{Bsf}(3,2)}{\sqrt{7}} }$$\color{darkred}{ \frac{\text{Asf}(3,3)}{\sqrt{7}} }$
$ {Y_{-1}^{(1)}} $$\color{darkred}{ -\frac{\text{Asp}(1,1)}{\sqrt{3}} }$$ \text{App}(0,0)-\frac{1}{5} \text{App}(2,0) $$ \frac{1}{5} i \sqrt{3} \text{Bpp}(2,1) $$ -\frac{1}{5} \sqrt{6} \text{App}(2,2) $$\color{darkred}{ \frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1)-\sqrt{\frac{2}{5}} \text{Apd}(1,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{\text{Apd}(1,1)}{\sqrt{15}}-\frac{3}{7} \sqrt{\frac{2}{5}} \text{Apd}(3,1) }$$\color{darkred}{ \frac{1}{7} i \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ -\frac{3}{7} \text{Apd}(3,3) }$$ \frac{3 \text{Apf}(2,2)}{\sqrt{35}}-\frac{\text{Apf}(4,2)}{3 \sqrt{21}} $$ \frac{i \text{Bpf}(4,1)}{3 \sqrt{7}}-i \sqrt{\frac{6}{35}} \text{Bpf}(2,1) $$ \frac{3}{5} \sqrt{\frac{2}{7}} \text{Apf}(2,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0) $$ \frac{1}{3} i \sqrt{\frac{10}{21}} \text{Bpf}(4,1)-\frac{3 i \text{Bpf}(2,1)}{5 \sqrt{7}} $$ \frac{1}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$ \frac{1}{3} i \text{Bpf}(4,3) $$ -\frac{2 \text{Apf}(4,4)}{3 \sqrt{3}} $
$ {Y_{0}^{(1)}} $$\color{darkred}{ 0 }$$ -\frac{1}{5} i \sqrt{3} \text{Bpp}(2,1) $$ \text{App}(0,0)+\frac{2}{5} \text{App}(2,0) $$ -\frac{1}{5} i \sqrt{3} \text{Bpp}(2,1) $$\color{darkred}{ \frac{1}{7} i \sqrt{3} \text{Bpd}(3,2) }$$\color{darkred}{ -\frac{\text{Apd}(1,1)}{\sqrt{5}}-\frac{2}{7} \sqrt{\frac{6}{5}} \text{Apd}(3,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{\text{Apd}(1,1)}{\sqrt{5}}+\frac{2}{7} \sqrt{\frac{6}{5}} \text{Apd}(3,1) }$$\color{darkred}{ -\frac{1}{7} i \sqrt{3} \text{Bpd}(3,2) }$$ -\frac{i \text{Bpf}(4,3)}{3 \sqrt{3}} $$ \sqrt{\frac{3}{35}} \text{Apf}(2,2)+\frac{2 \text{Apf}(4,2)}{3 \sqrt{7}} $$ -\frac{2}{5} i \sqrt{\frac{6}{7}} \text{Bpf}(2,1)-\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bpf}(4,1) $$ \frac{3}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,0)+\frac{4 \text{Apf}(4,0)}{3 \sqrt{21}} $$ -\frac{2}{5} i \sqrt{\frac{6}{7}} \text{Bpf}(2,1)-\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bpf}(4,1) $$ \sqrt{\frac{3}{35}} \text{Apf}(2,2)+\frac{2 \text{Apf}(4,2)}{3 \sqrt{7}} $$ -\frac{i \text{Bpf}(4,3)}{3 \sqrt{3}} $
$ {Y_{1}^{(1)}} $$\color{darkred}{ \frac{\text{Asp}(1,1)}{\sqrt{3}} }$$ -\frac{1}{5} \sqrt{6} \text{App}(2,2) $$ \frac{1}{5} i \sqrt{3} \text{Bpp}(2,1) $$ \text{App}(0,0)-\frac{1}{5} \text{App}(2,0) $$\color{darkred}{ \frac{3}{7} \text{Apd}(3,3) }$$\color{darkred}{ -\frac{1}{7} i \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ \frac{3}{7} \sqrt{\frac{2}{5}} \text{Apd}(3,1)-\frac{\text{Apd}(1,1)}{\sqrt{15}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \sqrt{\frac{2}{5}} \text{Apd}(1,1)-\frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1) }$$ -\frac{2 \text{Apf}(4,4)}{3 \sqrt{3}} $$ \frac{1}{3} i \text{Bpf}(4,3) $$ \frac{1}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$ \frac{1}{3} i \sqrt{\frac{10}{21}} \text{Bpf}(4,1)-\frac{3 i \text{Bpf}(2,1)}{5 \sqrt{7}} $$ \frac{3}{5} \sqrt{\frac{2}{7}} \text{Apf}(2,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0) $$ \frac{i \text{Bpf}(4,1)}{3 \sqrt{7}}-i \sqrt{\frac{6}{35}} \text{Bpf}(2,1) $$ \frac{3 \text{Apf}(2,2)}{\sqrt{35}}-\frac{\text{Apf}(4,2)}{3 \sqrt{21}} $
$ {Y_{-2}^{(2)}} $$ \frac{\text{Asd}(2,2)}{\sqrt{5}} $$\color{darkred}{ \frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1)-\sqrt{\frac{2}{5}} \text{Apd}(1,1) }$$\color{darkred}{ -\frac{1}{7} i \sqrt{3} \text{Bpd}(3,2) }$$\color{darkred}{ \frac{3}{7} \text{Apd}(3,3) }$$ \text{Add}(0,0)-\frac{2}{7} \text{Add}(2,0)+\frac{1}{21} \text{Add}(4,0) $$ \frac{1}{7} i \sqrt{6} \text{Bdd}(2,1)-\frac{1}{21} i \sqrt{5} \text{Bdd}(4,1) $$ \frac{1}{7} \sqrt{\frac{5}{3}} \text{Add}(4,2)-\frac{2}{7} \text{Add}(2,2) $$ -\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ \frac{1}{3} \sqrt{\frac{10}{7}} \text{Add}(4,4) $$\color{darkred}{ -\sqrt{\frac{3}{7}} \text{Adf}(1,1)+\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,1)-\frac{1}{33} \sqrt{\frac{5}{7}} \text{Adf}(5,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{\text{Adf}(1,1)}{\sqrt{35}}-2 \sqrt{\frac{2}{105}} \text{Adf}(3,1)+\frac{5 \text{Adf}(5,1)}{11 \sqrt{21}} }$$\color{darkred}{ \frac{2 i \text{Bdf}(3,2)}{3 \sqrt{7}}-\frac{5}{33} i \text{Bdf}(5,2) }$$\color{darkred}{ \frac{5}{33} \sqrt{2} \text{Adf}(5,3)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,3) }$$\color{darkred}{ -\frac{1}{11} i \sqrt{10} \text{Bdf}(5,4) }$$\color{darkred}{ \frac{5}{11} \sqrt{\frac{2}{3}} \text{Adf}(5,5) }$
$ {Y_{-1}^{(2)}} $$ \frac{i \text{Bsd}(2,1)}{\sqrt{5}} $$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Apd}(1,1)}{\sqrt{5}}-\frac{2}{7} \sqrt{\frac{6}{5}} \text{Apd}(3,1) }$$\color{darkred}{ \frac{1}{7} i \sqrt{6} \text{Bpd}(3,2) }$$ \frac{1}{21} i \sqrt{5} \text{Bdd}(4,1)-\frac{1}{7} i \sqrt{6} \text{Bdd}(2,1) $$ \text{Add}(0,0)+\frac{1}{7} \text{Add}(2,0)-\frac{4}{21} \text{Add}(4,0) $$ \frac{1}{7} i \text{Bdd}(2,1)+\frac{1}{7} i \sqrt{\frac{10}{3}} \text{Bdd}(4,1) $$ -\frac{1}{7} \sqrt{6} \text{Add}(2,2)-\frac{2}{21} \sqrt{10} \text{Add}(4,2) $$ \frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$\color{darkred}{ \frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdf}(3,2)-\frac{1}{33} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \sqrt{\frac{3}{35}} \text{Adf}(1,1)-\frac{1}{3} \sqrt{\frac{2}{35}} \text{Adf}(3,1)-\frac{20 \text{Adf}(5,1)}{33 \sqrt{7}} }$$\color{darkred}{ \frac{i \text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 i \text{Bdf}(5,2)}{11 \sqrt{3}} }$$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ \frac{2}{11} i \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$
$ {Y_{0}^{(2)}} $$ \frac{\text{Asd}(2,0)}{\sqrt{5}} $$\color{darkred}{ \frac{\text{Apd}(1,1)}{\sqrt{15}}-\frac{3}{7} \sqrt{\frac{2}{5}} \text{Apd}(3,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{3}{7} \sqrt{\frac{2}{5}} \text{Apd}(3,1)-\frac{\text{Apd}(1,1)}{\sqrt{15}} }$$ \frac{1}{7} \sqrt{\frac{5}{3}} \text{Add}(4,2)-\frac{2}{7} \text{Add}(2,2) $$ -\frac{1}{7} i \text{Bdd}(2,1)-\frac{1}{7} i \sqrt{\frac{10}{3}} \text{Bdd}(4,1) $$ \text{Add}(0,0)+\frac{2}{7} \text{Add}(2,0)+\frac{2}{7} \text{Add}(4,0) $$ -\frac{1}{7} i \text{Bdd}(2,1)-\frac{1}{7} i \sqrt{\frac{10}{3}} \text{Bdd}(4,1) $$ \frac{1}{7} \sqrt{\frac{5}{3}} \text{Add}(4,2)-\frac{2}{7} \text{Add}(2,2) $$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{2}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ \frac{1}{11} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ -\sqrt{\frac{6}{35}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{35}}-\frac{5}{11} \sqrt{\frac{2}{7}} \text{Adf}(5,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ \sqrt{\frac{6}{35}} \text{Adf}(1,1)+\frac{\text{Adf}(3,1)}{\sqrt{35}}+\frac{5}{11} \sqrt{\frac{2}{7}} \text{Adf}(5,1) }$$\color{darkred}{ -\frac{1}{11} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ \frac{2}{33} \sqrt{5} \text{Adf}(5,3)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3) }$
$ {Y_{1}^{(2)}} $$ \frac{i \text{Bsd}(2,1)}{\sqrt{5}} $$\color{darkred}{ -\frac{1}{7} i \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ \frac{\text{Apd}(1,1)}{\sqrt{5}}+\frac{2}{7} \sqrt{\frac{6}{5}} \text{Apd}(3,1) }$$\color{darkred}{ 0 }$$ \frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ -\frac{1}{7} \sqrt{6} \text{Add}(2,2)-\frac{2}{21} \sqrt{10} \text{Add}(4,2) $$ \frac{1}{7} i \text{Bdd}(2,1)+\frac{1}{7} i \sqrt{\frac{10}{3}} \text{Bdd}(4,1) $$ \text{Add}(0,0)+\frac{1}{7} \text{Add}(2,0)-\frac{4}{21} \text{Add}(4,0) $$ \frac{1}{21} i \sqrt{5} \text{Bdd}(4,1)-\frac{1}{7} i \sqrt{6} \text{Bdd}(2,1) $$\color{darkred}{ -\frac{2}{11} i \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)+\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ -\frac{i \text{Bdf}(3,2)}{\sqrt{21}}-\frac{5 i \text{Bdf}(5,2)}{11 \sqrt{3}} }$$\color{darkred}{ -\sqrt{\frac{3}{35}} \text{Adf}(1,1)+\frac{1}{3} \sqrt{\frac{2}{35}} \text{Adf}(3,1)+\frac{20 \text{Adf}(5,1)}{33 \sqrt{7}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \sqrt{\frac{2}{7}} \text{Adf}(1,1)+\frac{\text{Adf}(3,1)}{\sqrt{21}}-\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1) }$$\color{darkred}{ \frac{1}{33} i \sqrt{5} \text{Bdf}(5,2)-\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdf}(3,2) }$
$ {Y_{2}^{(2)}} $$ \frac{\text{Asd}(2,2)}{\sqrt{5}} $$\color{darkred}{ -\frac{3}{7} \text{Apd}(3,3) }$$\color{darkred}{ \frac{1}{7} i \sqrt{3} \text{Bpd}(3,2) }$$\color{darkred}{ \sqrt{\frac{2}{5}} \text{Apd}(1,1)-\frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1) }$$ \frac{1}{3} \sqrt{\frac{10}{7}} \text{Add}(4,4) $$ -\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ \frac{1}{7} \sqrt{\frac{5}{3}} \text{Add}(4,2)-\frac{2}{7} \text{Add}(2,2) $$ \frac{1}{7} i \sqrt{6} \text{Bdd}(2,1)-\frac{1}{21} i \sqrt{5} \text{Bdd}(4,1) $$ \text{Add}(0,0)-\frac{2}{7} \text{Add}(2,0)+\frac{1}{21} \text{Add}(4,0) $$\color{darkred}{ -\frac{5}{11} \sqrt{\frac{2}{3}} \text{Adf}(5,5) }$$\color{darkred}{ \frac{1}{11} i \sqrt{10} \text{Bdf}(5,4) }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,3)-\frac{5}{33} \sqrt{2} \text{Adf}(5,3) }$$\color{darkred}{ \frac{5}{33} i \text{Bdf}(5,2)-\frac{2 i \text{Bdf}(3,2)}{3 \sqrt{7}} }$$\color{darkred}{ -\frac{\text{Adf}(1,1)}{\sqrt{35}}+2 \sqrt{\frac{2}{105}} \text{Adf}(3,1)-\frac{5 \text{Adf}(5,1)}{11 \sqrt{21}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \sqrt{\frac{3}{7}} \text{Adf}(1,1)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,1)+\frac{1}{33} \sqrt{\frac{5}{7}} \text{Adf}(5,1) }$
$ {Y_{-3}^{(3)}} $$\color{darkred}{ -\frac{\text{Asf}(3,3)}{\sqrt{7}} }$$ \frac{3 \text{Apf}(2,2)}{\sqrt{35}}-\frac{\text{Apf}(4,2)}{3 \sqrt{21}} $$ \frac{i \text{Bpf}(4,3)}{3 \sqrt{3}} $$ -\frac{2 \text{Apf}(4,4)}{3 \sqrt{3}} $$\color{darkred}{ -\sqrt{\frac{3}{7}} \text{Adf}(1,1)+\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,1)-\frac{1}{33} \sqrt{\frac{5}{7}} \text{Adf}(5,1) }$$\color{darkred}{ \frac{1}{33} i \sqrt{5} \text{Bdf}(5,2)-\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdf}(3,2) }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{2}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ \frac{2}{11} i \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$$\color{darkred}{ -\frac{5}{11} \sqrt{\frac{2}{3}} \text{Adf}(5,5) }$$ \text{Aff}(0,0)-\frac{1}{3} \text{Aff}(2,0)+\frac{1}{11} \text{Aff}(4,0)-\frac{5}{429} \text{Aff}(6,0) $$ \frac{1}{3} i \text{Bff}(2,1)-\frac{1}{11} i \sqrt{\frac{10}{3}} \text{Bff}(4,1)+\frac{5}{429} i \sqrt{7} \text{Bff}(6,1) $$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)+\frac{1}{11} \sqrt{6} \text{Aff}(4,2)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2) $$ \frac{10}{143} i \sqrt{\frac{7}{3}} \text{Bff}(6,3)-\frac{1}{11} i \sqrt{7} \text{Bff}(4,3) $$ \frac{1}{11} \sqrt{\frac{14}{3}} \text{Aff}(4,4)-\frac{5}{143} \sqrt{\frac{70}{3}} \text{Aff}(6,4) $$ \frac{5}{13} i \sqrt{\frac{14}{33}} \text{Bff}(6,5) $$ -\frac{10}{13} \sqrt{\frac{7}{33}} \text{Aff}(6,6) $
$ {Y_{-2}^{(3)}} $$\color{darkred}{ -\frac{i \text{Bsf}(3,2)}{\sqrt{7}} }$$ i \sqrt{\frac{6}{35}} \text{Bpf}(2,1)-\frac{i \text{Bpf}(4,1)}{3 \sqrt{7}} $$ \sqrt{\frac{3}{35}} \text{Apf}(2,2)+\frac{2 \text{Apf}(4,2)}{3 \sqrt{7}} $$ -\frac{1}{3} i \text{Bpf}(4,3) $$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1) }$$\color{darkred}{ -\frac{1}{11} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)+\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ -\frac{1}{11} i \sqrt{10} \text{Bdf}(5,4) }$$ -\frac{1}{3} i \text{Bff}(2,1)+\frac{1}{11} i \sqrt{\frac{10}{3}} \text{Bff}(4,1)-\frac{5}{429} i \sqrt{7} \text{Bff}(6,1) $$ \text{Aff}(0,0)-\frac{7}{33} \text{Aff}(4,0)+\frac{10}{143} \text{Aff}(6,0) $$ \frac{i \text{Bff}(2,1)}{\sqrt{15}}+\frac{4}{33} i \sqrt{2} \text{Bff}(4,1)-\frac{5}{143} i \sqrt{\frac{35}{3}} \text{Bff}(6,1) $$ -\frac{2 \text{Aff}(2,2)}{3 \sqrt{5}}-\frac{\text{Aff}(4,2)}{11 \sqrt{3}}+\frac{20}{429} \sqrt{14} \text{Aff}(6,2) $$ -\frac{1}{33} i \sqrt{14} \text{Bff}(4,3)-\frac{5}{143} i \sqrt{42} \text{Bff}(6,3) $$ \frac{1}{33} \sqrt{70} \text{Aff}(4,4)+\frac{10}{143} \sqrt{14} \text{Aff}(6,4) $$ -\frac{5}{13} i \sqrt{\frac{14}{33}} \text{Bff}(6,5) $
$ {Y_{-1}^{(3)}} $$\color{darkred}{ -\frac{\text{Asf}(3,1)}{\sqrt{7}} }$$ \frac{3}{5} \sqrt{\frac{2}{7}} \text{Apf}(2,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0) $$ \frac{2}{5} i \sqrt{\frac{6}{7}} \text{Bpf}(2,1)+\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bpf}(4,1) $$ \frac{1}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$\color{darkred}{ \frac{\text{Adf}(1,1)}{\sqrt{35}}-2 \sqrt{\frac{2}{105}} \text{Adf}(3,1)+\frac{5 \text{Adf}(5,1)}{11 \sqrt{21}} }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{6}{35}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{35}}-\frac{5}{11} \sqrt{\frac{2}{7}} \text{Adf}(5,1) }$$\color{darkred}{ \frac{i \text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 i \text{Bdf}(5,2)}{11 \sqrt{3}} }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,3)-\frac{5}{33} \sqrt{2} \text{Adf}(5,3) }$$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)+\frac{1}{11} \sqrt{6} \text{Aff}(4,2)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2) $$ -\frac{i \text{Bff}(2,1)}{\sqrt{15}}-\frac{4}{33} i \sqrt{2} \text{Bff}(4,1)+\frac{5}{143} i \sqrt{\frac{35}{3}} \text{Bff}(6,1) $$ \text{Aff}(0,0)+\frac{1}{5} \text{Aff}(2,0)+\frac{1}{33} \text{Aff}(4,0)-\frac{25}{143} \text{Aff}(6,0) $$ \frac{1}{15} i \sqrt{2} \text{Bff}(2,1)+\frac{1}{11} i \sqrt{\frac{5}{3}} \text{Bff}(4,1)+\frac{25}{429} i \sqrt{14} \text{Bff}(6,1) $$ -\frac{2}{5} \sqrt{\frac{2}{3}} \text{Aff}(2,2)-\frac{2}{33} \sqrt{10} \text{Aff}(4,2)-\frac{10}{143} \sqrt{\frac{35}{3}} \text{Aff}(6,2) $$ \frac{1}{33} i \sqrt{14} \text{Bff}(4,3)+\frac{5}{143} i \sqrt{42} \text{Bff}(6,3) $$ \frac{1}{11} \sqrt{\frac{14}{3}} \text{Aff}(4,4)-\frac{5}{143} \sqrt{\frac{70}{3}} \text{Aff}(6,4) $
$ {Y_{0}^{(3)}} $$\color{darkred}{ 0 }$$ \frac{3 i \text{Bpf}(2,1)}{5 \sqrt{7}}-\frac{1}{3} i \sqrt{\frac{10}{21}} \text{Bpf}(4,1) $$ \frac{3}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,0)+\frac{4 \text{Apf}(4,0)}{3 \sqrt{21}} $$ \frac{3 i \text{Bpf}(2,1)}{5 \sqrt{7}}-\frac{1}{3} i \sqrt{\frac{10}{21}} \text{Bpf}(4,1) $$\color{darkred}{ \frac{5}{33} i \text{Bdf}(5,2)-\frac{2 i \text{Bdf}(3,2)}{3 \sqrt{7}} }$$\color{darkred}{ \sqrt{\frac{3}{35}} \text{Adf}(1,1)-\frac{1}{3} \sqrt{\frac{2}{35}} \text{Adf}(3,1)-\frac{20 \text{Adf}(5,1)}{33 \sqrt{7}} }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{3}{35}} \text{Adf}(1,1)+\frac{1}{3} \sqrt{\frac{2}{35}} \text{Adf}(3,1)+\frac{20 \text{Adf}(5,1)}{33 \sqrt{7}} }$$\color{darkred}{ \frac{2 i \text{Bdf}(3,2)}{3 \sqrt{7}}-\frac{5}{33} i \text{Bdf}(5,2) }$$ \frac{1}{11} i \sqrt{7} \text{Bff}(4,3)-\frac{10}{143} i \sqrt{\frac{7}{3}} \text{Bff}(6,3) $$ -\frac{2 \text{Aff}(2,2)}{3 \sqrt{5}}-\frac{\text{Aff}(4,2)}{11 \sqrt{3}}+\frac{20}{429} \sqrt{14} \text{Aff}(6,2) $$ -\frac{1}{15} i \sqrt{2} \text{Bff}(2,1)-\frac{1}{11} i \sqrt{\frac{5}{3}} \text{Bff}(4,1)-\frac{25}{429} i \sqrt{14} \text{Bff}(6,1) $$ \text{Aff}(0,0)+\frac{4}{15} \text{Aff}(2,0)+\frac{2}{11} \text{Aff}(4,0)+\frac{100}{429} \text{Aff}(6,0) $$ -\frac{1}{15} i \sqrt{2} \text{Bff}(2,1)-\frac{1}{11} i \sqrt{\frac{5}{3}} \text{Bff}(4,1)-\frac{25}{429} i \sqrt{14} \text{Bff}(6,1) $$ -\frac{2 \text{Aff}(2,2)}{3 \sqrt{5}}-\frac{\text{Aff}(4,2)}{11 \sqrt{3}}+\frac{20}{429} \sqrt{14} \text{Aff}(6,2) $$ \frac{1}{11} i \sqrt{7} \text{Bff}(4,3)-\frac{10}{143} i \sqrt{\frac{7}{3}} \text{Bff}(6,3) $
$ {Y_{1}^{(3)}} $$\color{darkred}{ \frac{\text{Asf}(3,1)}{\sqrt{7}} }$$ \frac{1}{5} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$ \frac{2}{5} i \sqrt{\frac{6}{7}} \text{Bpf}(2,1)+\frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bpf}(4,1) $$ \frac{3}{5} \sqrt{\frac{2}{7}} \text{Apf}(2,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0) $$\color{darkred}{ \frac{5}{33} \sqrt{2} \text{Adf}(5,3)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,3) }$$\color{darkred}{ -\frac{i \text{Bdf}(3,2)}{\sqrt{21}}-\frac{5 i \text{Bdf}(5,2)}{11 \sqrt{3}} }$$\color{darkred}{ \sqrt{\frac{6}{35}} \text{Adf}(1,1)+\frac{\text{Adf}(3,1)}{\sqrt{35}}+\frac{5}{11} \sqrt{\frac{2}{7}} \text{Adf}(5,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Adf}(1,1)}{\sqrt{35}}+2 \sqrt{\frac{2}{105}} \text{Adf}(3,1)-\frac{5 \text{Adf}(5,1)}{11 \sqrt{21}} }$$ \frac{1}{11} \sqrt{\frac{14}{3}} \text{Aff}(4,4)-\frac{5}{143} \sqrt{\frac{70}{3}} \text{Aff}(6,4) $$ \frac{1}{33} i \sqrt{14} \text{Bff}(4,3)+\frac{5}{143} i \sqrt{42} \text{Bff}(6,3) $$ -\frac{2}{5} \sqrt{\frac{2}{3}} \text{Aff}(2,2)-\frac{2}{33} \sqrt{10} \text{Aff}(4,2)-\frac{10}{143} \sqrt{\frac{35}{3}} \text{Aff}(6,2) $$ \frac{1}{15} i \sqrt{2} \text{Bff}(2,1)+\frac{1}{11} i \sqrt{\frac{5}{3}} \text{Bff}(4,1)+\frac{25}{429} i \sqrt{14} \text{Bff}(6,1) $$ \text{Aff}(0,0)+\frac{1}{5} \text{Aff}(2,0)+\frac{1}{33} \text{Aff}(4,0)-\frac{25}{143} \text{Aff}(6,0) $$ -\frac{i \text{Bff}(2,1)}{\sqrt{15}}-\frac{4}{33} i \sqrt{2} \text{Bff}(4,1)+\frac{5}{143} i \sqrt{\frac{35}{3}} \text{Bff}(6,1) $$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)+\frac{1}{11} \sqrt{6} \text{Aff}(4,2)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2) $
$ {Y_{2}^{(3)}} $$\color{darkred}{ \frac{i \text{Bsf}(3,2)}{\sqrt{7}} }$$ -\frac{1}{3} i \text{Bpf}(4,3) $$ \sqrt{\frac{3}{35}} \text{Apf}(2,2)+\frac{2 \text{Apf}(4,2)}{3 \sqrt{7}} $$ i \sqrt{\frac{6}{35}} \text{Bpf}(2,1)-\frac{i \text{Bpf}(4,1)}{3 \sqrt{7}} $$\color{darkred}{ \frac{1}{11} i \sqrt{10} \text{Bdf}(5,4) }$$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ \frac{1}{11} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ \sqrt{\frac{2}{7}} \text{Adf}(1,1)+\frac{\text{Adf}(3,1)}{\sqrt{21}}-\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1) }$$\color{darkred}{ 0 }$$ -\frac{5}{13} i \sqrt{\frac{14}{33}} \text{Bff}(6,5) $$ \frac{1}{33} \sqrt{70} \text{Aff}(4,4)+\frac{10}{143} \sqrt{14} \text{Aff}(6,4) $$ -\frac{1}{33} i \sqrt{14} \text{Bff}(4,3)-\frac{5}{143} i \sqrt{42} \text{Bff}(6,3) $$ -\frac{2 \text{Aff}(2,2)}{3 \sqrt{5}}-\frac{\text{Aff}(4,2)}{11 \sqrt{3}}+\frac{20}{429} \sqrt{14} \text{Aff}(6,2) $$ \frac{i \text{Bff}(2,1)}{\sqrt{15}}+\frac{4}{33} i \sqrt{2} \text{Bff}(4,1)-\frac{5}{143} i \sqrt{\frac{35}{3}} \text{Bff}(6,1) $$ \text{Aff}(0,0)-\frac{7}{33} \text{Aff}(4,0)+\frac{10}{143} \text{Aff}(6,0) $$ -\frac{1}{3} i \text{Bff}(2,1)+\frac{1}{11} i \sqrt{\frac{10}{3}} \text{Bff}(4,1)-\frac{5}{429} i \sqrt{7} \text{Bff}(6,1) $
$ {Y_{3}^{(3)}} $$\color{darkred}{ \frac{\text{Asf}(3,3)}{\sqrt{7}} }$$ -\frac{2 \text{Apf}(4,4)}{3 \sqrt{3}} $$ \frac{i \text{Bpf}(4,3)}{3 \sqrt{3}} $$ \frac{3 \text{Apf}(2,2)}{\sqrt{35}}-\frac{\text{Apf}(4,2)}{3 \sqrt{21}} $$\color{darkred}{ \frac{5}{11} \sqrt{\frac{2}{3}} \text{Adf}(5,5) }$$\color{darkred}{ -\frac{2}{11} i \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$$\color{darkred}{ \frac{2}{33} \sqrt{5} \text{Adf}(5,3)-\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3) }$$\color{darkred}{ \frac{1}{3} i \sqrt{\frac{5}{7}} \text{Bdf}(3,2)-\frac{1}{33} i \sqrt{5} \text{Bdf}(5,2) }$$\color{darkred}{ \sqrt{\frac{3}{7}} \text{Adf}(1,1)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Adf}(3,1)+\frac{1}{33} \sqrt{\frac{5}{7}} \text{Adf}(5,1) }$$ -\frac{10}{13} \sqrt{\frac{7}{33}} \text{Aff}(6,6) $$ \frac{5}{13} i \sqrt{\frac{14}{33}} \text{Bff}(6,5) $$ \frac{1}{11} \sqrt{\frac{14}{3}} \text{Aff}(4,4)-\frac{5}{143} \sqrt{\frac{70}{3}} \text{Aff}(6,4) $$ \frac{10}{143} i \sqrt{\frac{7}{3}} \text{Bff}(6,3)-\frac{1}{11} i \sqrt{7} \text{Bff}(4,3) $$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)+\frac{1}{11} \sqrt{6} \text{Aff}(4,2)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2) $$ \frac{1}{3} i \text{Bff}(2,1)-\frac{1}{11} i \sqrt{\frac{10}{3}} \text{Bff}(4,1)+\frac{5}{429} i \sqrt{7} \text{Bff}(6,1) $$ \text{Aff}(0,0)-\frac{1}{3} \text{Aff}(2,0)+\frac{1}{11} \text{Aff}(4,0)-\frac{5}{429} \text{Aff}(6,0) $

Rotation matrix to symmetry adapted functions (choice is not unique)

Instead of a basis of spherical harmonics one can chose any other basis, which is given by a unitary transformation. Here we choose a rotation that simplifies the representation of the crystal field

$ $ $ {Y_{0}^{(0)}} $ $ {Y_{-1}^{(1)}} $ $ {Y_{0}^{(1)}} $ $ {Y_{1}^{(1)}} $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ \text{s} $$ 1 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ p_z $$\color{darkred}{ 0 }$$ 0 $$ 1 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $
$ p_x $$\color{darkred}{ 0 }$$ \frac{1}{\sqrt{2}} $$ 0 $$ -\frac{1}{\sqrt{2}} $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $
$ p_y $$\color{darkred}{ 0 }$$ \frac{i}{\sqrt{2}} $$ 0 $$ \frac{i}{\sqrt{2}} $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $$ 0 $
$ d_{\text{yz}} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ d_{\text{xz}} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ \frac{1}{\sqrt{2}} $$ 0 $$ -\frac{1}{\sqrt{2}} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ d_{3x^2-r^2} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ \frac{\sqrt{\frac{3}{2}}}{2} $$ 0 $$ -\frac{1}{2} $$ 0 $$ \frac{\sqrt{\frac{3}{2}}}{2} $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ d_{\text{xz}} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ \frac{i}{\sqrt{2}} $$ 0 $$ 0 $$ 0 $$ -\frac{i}{\sqrt{2}} $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ d_{y^2-z^2} $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ -\frac{1}{2 \sqrt{2}} $$ 0 $$ -\frac{\sqrt{3}}{2} $$ 0 $$ -\frac{1}{2 \sqrt{2}} $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$
$ f_{z\left(3y^2-z^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{\frac{5}{2}}}{2} $$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $
$ f_{\text{xyz}} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $$ 0 $$ 0 $$ -\frac{i}{\sqrt{2}} $$ 0 $
$ f_{z\left(5x^2-r^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $$ -\frac{\sqrt{\frac{3}{2}}}{2} $$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $
$ f_{x\left(5x^2-3r^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ \frac{\sqrt{5}}{4} $$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $$ \frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{5}}{4} $
$ f_{y\left(5x^2-r^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ \frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ \frac{1}{4} i \sqrt{\frac{15}{2}} $
$ f_{x\left(y^2-z^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ -\frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{5}}{4} $$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $$ \frac{\sqrt{3}}{4} $
$ f_{y\left(y^2-3z^2\right)} $$\color{darkred}{ 0 }$$ 0 $$ 0 $$ 0 $$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$\color{darkred}{ 0 }$$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ -\frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $

One particle coupling on a basis of symmetry adapted functions

After rotation we find

$ $ $ \text{s} $ $ p_z $ $ p_x $ $ p_y $ $ d_{\text{yz}} $ $ d_{\text{xz}} $ $ d_{3x^2-r^2} $ $ d_{\text{xz}} $ $ d_{y^2-z^2} $ $ f_{z\left(3y^2-z^2\right)} $ $ f_{\text{xyz}} $ $ f_{z\left(5x^2-r^2\right)} $ $ f_{x\left(5x^2-3r^2\right)} $ $ f_{y\left(5x^2-r^2\right)} $ $ f_{x\left(y^2-z^2\right)} $ $ f_{y\left(y^2-3z^2\right)} $
$ \text{s} $$ \text{Ass}(0,0) $$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{3}} \text{Asp}(1,1) }$$\color{darkred}{ 0 }$$ \sqrt{\frac{2}{5}} \text{Bsd}(2,1) $$ 0 $$ \sqrt{\frac{3}{10}} \text{Asd}(2,2)-\frac{\text{Asd}(2,0)}{2 \sqrt{5}} $$ 0 $$ -\frac{1}{2} \sqrt{\frac{3}{5}} \text{Asd}(2,0)-\frac{\text{Asd}(2,2)}{\sqrt{10}} $$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Bsf}(3,2) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{2} \sqrt{\frac{3}{7}} \text{Asf}(3,1)-\frac{1}{2} \sqrt{\frac{5}{7}} \text{Asf}(3,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{2} \sqrt{\frac{5}{7}} \text{Asf}(3,1)+\frac{1}{2} \sqrt{\frac{3}{7}} \text{Asf}(3,3) }$$\color{darkred}{ 0 }$
$ p_z $$\color{darkred}{ 0 }$$ \text{App}(0,0)+\frac{2}{5} \text{App}(2,0) $$ 0 $$ \frac{1}{5} \sqrt{6} \text{Bpp}(2,1) $$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{5}} \text{Apd}(1,1)-\frac{4}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ 0 }$$ -\frac{3}{2} \sqrt{\frac{3}{70}} \text{Apf}(2,0)-\frac{3 \text{Apf}(2,2)}{2 \sqrt{35}}-\frac{1}{3} \sqrt{\frac{10}{21}} \text{Apf}(4,0)-\frac{\text{Apf}(4,2)}{\sqrt{21}} $$ 0 $$ -\frac{9 \text{Apf}(2,0)}{10 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0)+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$ 0 $$ -\frac{1}{5} \sqrt{\frac{3}{7}} \text{Bpf}(2,1)-\frac{1}{6} \sqrt{\frac{5}{14}} \text{Bpf}(4,1)+\frac{1}{6} \sqrt{\frac{5}{2}} \text{Bpf}(4,3) $$ 0 $$ -\frac{3 \text{Bpf}(2,1)}{\sqrt{35}}-\frac{5 \text{Bpf}(4,1)}{2 \sqrt{42}}-\frac{\text{Bpf}(4,3)}{6 \sqrt{6}} $
$ p_x $$\color{darkred}{ -\sqrt{\frac{2}{3}} \text{Asp}(1,1) }$$ 0 $$ \text{App}(0,0)-\frac{1}{5} \text{App}(2,0)+\frac{1}{5} \sqrt{6} \text{App}(2,2) $$ 0 $$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ 0 }$$\color{darkred}{ -2 \sqrt{\frac{2}{15}} \text{Apd}(1,1)+\frac{9 \text{Apd}(3,1)}{14 \sqrt{5}}-\frac{3}{14} \sqrt{3} \text{Apd}(3,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{14} \sqrt{15} \text{Apd}(3,1)+\frac{3}{14} \text{Apd}(3,3) }$$ 0 $$ \sqrt{\frac{6}{35}} \text{Bpf}(2,1)-\frac{\text{Bpf}(4,1)}{3 \sqrt{7}}+\frac{1}{3} \text{Bpf}(4,3) $$ 0 $$ -\frac{3}{10} \sqrt{\frac{3}{7}} \text{Apf}(2,0)+\frac{9 \text{Apf}(2,2)}{5 \sqrt{14}}+\frac{\text{Apf}(4,0)}{2 \sqrt{21}}-\frac{1}{3} \sqrt{\frac{10}{21}} \text{Apf}(4,2)+\frac{1}{3} \sqrt{\frac{5}{6}} \text{Apf}(4,4) $$ 0 $$ -\frac{3 \text{Apf}(2,0)}{2 \sqrt{35}}-\sqrt{\frac{3}{70}} \text{Apf}(2,2)+\frac{1}{6} \sqrt{\frac{5}{7}} \text{Apf}(4,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,2)-\frac{\text{Apf}(4,4)}{3 \sqrt{2}} $$ 0 $
$ p_y $$\color{darkred}{ 0 }$$ \frac{1}{5} \sqrt{6} \text{Bpp}(2,1) $$ 0 $$ \text{App}(0,0)-\frac{1}{5} \text{App}(2,0)-\frac{1}{5} \sqrt{6} \text{App}(2,2) $$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{5}} \text{Apd}(1,1)+\frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1)+\frac{3}{7} \text{Apd}(3,3) }$$\color{darkred}{ 0 }$$ \frac{3 \text{Bpf}(2,1)}{\sqrt{35}}-\frac{13 \text{Bpf}(4,1)}{6 \sqrt{42}}-\frac{\text{Bpf}(4,3)}{2 \sqrt{6}} $$ 0 $$ -\frac{1}{5} \sqrt{\frac{3}{7}} \text{Bpf}(2,1)-\frac{1}{6} \sqrt{\frac{5}{14}} \text{Bpf}(4,1)+\frac{1}{6} \sqrt{\frac{5}{2}} \text{Bpf}(4,3) $$ 0 $$ -\frac{3 \text{Apf}(2,0)}{10 \sqrt{14}}+\frac{1}{10} \sqrt{21} \text{Apf}(2,2)+\frac{\text{Apf}(4,0)}{6 \sqrt{14}}-\frac{1}{6} \sqrt{5} \text{Apf}(4,4) $$ 0 $$ -\frac{3}{2} \sqrt{\frac{3}{70}} \text{Apf}(2,0)-\frac{3 \text{Apf}(2,2)}{2 \sqrt{35}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Apf}(4,0)+\frac{4 \text{Apf}(4,2)}{3 \sqrt{21}}+\frac{\text{Apf}(4,4)}{6 \sqrt{3}} $
$ d_{\text{yz}} $$ \sqrt{\frac{2}{5}} \text{Bsd}(2,1) $$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ 0 }$$ \text{Add}(0,0)+\frac{1}{7} \text{Add}(2,0)-\frac{1}{7} \sqrt{6} \text{Add}(2,2)-\frac{4}{21} \text{Add}(4,0)-\frac{2}{21} \sqrt{10} \text{Add}(4,2) $$ 0 $$ -\frac{2}{7} \sqrt{2} \text{Bdd}(2,1)-\frac{1}{14} \sqrt{\frac{5}{3}} \text{Bdd}(4,1)+\frac{1}{2} \sqrt{\frac{5}{21}} \text{Bdd}(4,3) $$ 0 $$ -\frac{1}{6} \sqrt{5} \text{Bdd}(4,1)-\frac{1}{6} \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)+\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1)+\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{2}{3} \sqrt{\frac{2}{7}} \text{Bdf}(3,2)+\frac{5 \text{Bdf}(5,2)}{33 \sqrt{2}}-\frac{5 \text{Bdf}(5,4)}{11 \sqrt{6}} }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,2)+\frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$
$ d_{\text{xz}} $$ 0 $$\color{darkred}{ -\sqrt{\frac{2}{5}} \text{Apd}(1,1)-\frac{4}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$ 0 $$ \text{Add}(0,0)+\frac{1}{7} \text{Add}(2,0)+\frac{1}{7} \sqrt{6} \text{Add}(2,2)-\frac{4}{21} \text{Add}(4,0)+\frac{2}{21} \sqrt{10} \text{Add}(4,2) $$ 0 $$ \frac{1}{7} \sqrt{6} \text{Bdd}(2,1)-\frac{1}{21} \sqrt{5} \text{Bdd}(4,1)+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ 0 $$\color{darkred}{ \frac{5 \text{Adf}(3,1)}{6 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Adf}(3,3)+\frac{1}{33} \sqrt{35} \text{Adf}(5,1)+\frac{1}{11} \sqrt{\frac{10}{3}} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{4 \text{Adf}(1,1)}{\sqrt{35}}-\frac{1}{2} \sqrt{\frac{3}{70}} \text{Adf}(3,1)-\frac{5 \text{Adf}(3,3)}{6 \sqrt{14}}+\frac{5}{11} \sqrt{\frac{3}{7}} \text{Adf}(5,1)-\frac{5}{33} \sqrt{2} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 \text{Bdf}(5,2)}{22 \sqrt{3}}-\frac{5}{22} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdf}(3,2)+\frac{7}{66} \sqrt{5} \text{Bdf}(5,2)+\frac{1}{22} \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$
$ d_{3x^2-r^2} $$ \sqrt{\frac{3}{10}} \text{Asd}(2,2)-\frac{\text{Asd}(2,0)}{2 \sqrt{5}} $$\color{darkred}{ 0 }$$\color{darkred}{ -2 \sqrt{\frac{2}{15}} \text{Apd}(1,1)+\frac{9 \text{Apd}(3,1)}{14 \sqrt{5}}-\frac{3}{14} \sqrt{3} \text{Apd}(3,3) }$$\color{darkred}{ 0 }$$ -\frac{2}{7} \sqrt{2} \text{Bdd}(2,1)-\frac{1}{14} \sqrt{\frac{5}{3}} \text{Bdd}(4,1)+\frac{1}{2} \sqrt{\frac{5}{21}} \text{Bdd}(4,3) $$ 0 $$ \text{Add}(0,0)-\frac{1}{7} \text{Add}(2,0)+\frac{1}{7} \sqrt{6} \text{Add}(2,2)+\frac{3}{28} \text{Add}(4,0)-\frac{1}{7} \sqrt{\frac{5}{2}} \text{Add}(4,2)+\frac{1}{2} \sqrt{\frac{5}{14}} \text{Add}(4,4) $$ 0 $$ \frac{1}{7} \sqrt{3} \text{Add}(2,0)+\frac{1}{7} \sqrt{2} \text{Add}(2,2)+\frac{5 \text{Add}(4,0)}{28 \sqrt{3}}-\frac{1}{7} \sqrt{\frac{5}{6}} \text{Add}(4,2)-\frac{1}{2} \sqrt{\frac{5}{42}} \text{Add}(4,4) $$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,2)-\frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -3 \sqrt{\frac{2}{35}} \text{Adf}(1,1)+\frac{2 \text{Adf}(3,1)}{\sqrt{105}}-\frac{2 \text{Adf}(3,3)}{3 \sqrt{7}}-\frac{25 \text{Adf}(5,1)}{22 \sqrt{42}}+\frac{25}{132} \text{Adf}(5,3)-\frac{5}{44} \sqrt{5} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{22} \sqrt{\frac{35}{2}} \text{Adf}(5,1)+\frac{1}{44} \sqrt{15} \text{Adf}(5,3)+\frac{5}{44} \sqrt{3} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$
$ d_{\text{xz}} $$ 0 $$\color{darkred}{ -\frac{1}{7} \sqrt{6} \text{Bpd}(3,2) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{5}} \text{Apd}(1,1)+\frac{1}{7} \sqrt{\frac{3}{5}} \text{Apd}(3,1)+\frac{3}{7} \text{Apd}(3,3) }$$ 0 $$ \frac{1}{7} \sqrt{6} \text{Bdd}(2,1)-\frac{1}{21} \sqrt{5} \text{Bdd}(4,1)+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ 0 $$ \text{Add}(0,0)-\frac{2}{7} \text{Add}(2,0)+\frac{1}{21} \text{Add}(4,0)-\frac{1}{3} \sqrt{\frac{10}{7}} \text{Add}(4,4) $$ 0 $$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdf}(3,2)+\frac{5}{66} \sqrt{5} \text{Bdf}(5,2)+\frac{1}{22} \sqrt{15} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 \text{Bdf}(5,2)}{22 \sqrt{3}}-\frac{5}{22} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{4 \text{Adf}(1,1)}{\sqrt{35}}+\frac{1}{2} \sqrt{\frac{7}{30}} \text{Adf}(3,1)+\frac{\text{Adf}(3,3)}{6 \sqrt{14}}-\frac{5 \text{Adf}(5,1)}{22 \sqrt{21}}-\frac{5 \text{Adf}(5,3)}{66 \sqrt{2}}+\frac{5}{22} \sqrt{\frac{5}{2}} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{5 \text{Adf}(3,1)}{6 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Adf}(3,3)-\frac{1}{66} \sqrt{35} \text{Adf}(5,1)-\frac{5}{22} \sqrt{\frac{5}{6}} \text{Adf}(5,3)-\frac{5 \text{Adf}(5,5)}{22 \sqrt{6}} }$
$ d_{y^2-z^2} $$ -\frac{1}{2} \sqrt{\frac{3}{5}} \text{Asd}(2,0)-\frac{\text{Asd}(2,2)}{\sqrt{10}} $$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{14} \sqrt{15} \text{Apd}(3,1)+\frac{3}{14} \text{Apd}(3,3) }$$\color{darkred}{ 0 }$$ -\frac{1}{6} \sqrt{5} \text{Bdd}(4,1)-\frac{1}{6} \sqrt{\frac{5}{7}} \text{Bdd}(4,3) $$ 0 $$ \frac{1}{7} \sqrt{3} \text{Add}(2,0)+\frac{1}{7} \sqrt{2} \text{Add}(2,2)+\frac{5 \text{Add}(4,0)}{28 \sqrt{3}}-\frac{1}{7} \sqrt{\frac{5}{6}} \text{Add}(4,2)-\frac{1}{2} \sqrt{\frac{5}{42}} \text{Add}(4,4) $$ 0 $$ \text{Add}(0,0)+\frac{1}{7} \text{Add}(2,0)-\frac{1}{7} \sqrt{6} \text{Add}(2,2)+\frac{19}{84} \text{Add}(4,0)+\frac{1}{7} \sqrt{\frac{5}{2}} \text{Add}(4,2)+\frac{1}{6} \sqrt{\frac{5}{14}} \text{Add}(4,4) $$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,2)+\frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,1)-\frac{\text{Adf}(3,3)}{\sqrt{21}}-\frac{5}{66} \sqrt{\frac{7}{2}} \text{Adf}(5,1)+\frac{5 \text{Adf}(5,3)}{44 \sqrt{3}}+\frac{5}{44} \sqrt{\frac{5}{3}} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{13}{22} \sqrt{\frac{5}{42}} \text{Adf}(5,1)-\frac{1}{12} \sqrt{5} \text{Adf}(5,3)-\frac{5}{44} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$
$ f_{z\left(3y^2-z^2\right)} $$\color{darkred}{ 0 }$$ -\frac{3}{2} \sqrt{\frac{3}{70}} \text{Apf}(2,0)-\frac{3 \text{Apf}(2,2)}{2 \sqrt{35}}-\frac{1}{3} \sqrt{\frac{10}{21}} \text{Apf}(4,0)-\frac{\text{Apf}(4,2)}{\sqrt{21}} $$ 0 $$ \frac{3 \text{Bpf}(2,1)}{\sqrt{35}}-\frac{13 \text{Bpf}(4,1)}{6 \sqrt{42}}-\frac{\text{Bpf}(4,3)}{2 \sqrt{6}} $$\color{darkred}{ 0 }$$\color{darkred}{ \frac{5 \text{Adf}(3,1)}{6 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Adf}(3,3)+\frac{1}{33} \sqrt{35} \text{Adf}(5,1)+\frac{1}{11} \sqrt{\frac{10}{3}} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdf}(3,2)+\frac{5}{66} \sqrt{5} \text{Bdf}(5,2)+\frac{1}{22} \sqrt{15} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$ \text{Aff}(0,0)+\frac{1}{6} \text{Aff}(2,0)-\frac{\text{Aff}(2,2)}{\sqrt{6}}+\frac{3}{88} \text{Aff}(4,0)-\frac{1}{22} \sqrt{\frac{5}{2}} \text{Aff}(4,2)+\frac{1}{44} \sqrt{\frac{35}{2}} \text{Aff}(4,4)+\frac{295 \text{Aff}(6,0)}{1716}+\frac{10}{143} \sqrt{\frac{35}{3}} \text{Aff}(6,2)+\frac{15}{286} \sqrt{\frac{7}{2}} \text{Aff}(6,4) $$ 0 $$ \frac{\text{Aff}(2,0)}{2 \sqrt{15}}+\frac{\text{Aff}(2,2)}{3 \sqrt{10}}+\frac{13}{88} \sqrt{\frac{5}{3}} \text{Aff}(4,0)+\frac{\text{Aff}(4,2)}{22 \sqrt{6}}-\frac{5}{44} \sqrt{\frac{7}{6}} \text{Aff}(4,4)+\frac{35}{572} \sqrt{\frac{5}{3}} \text{Aff}(6,0)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2)-\frac{5}{286} \sqrt{\frac{105}{2}} \text{Aff}(6,4) $$ 0 $$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{2 \text{Bff}(4,1)}{11 \sqrt{3}}+\frac{2}{11} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{25 \sqrt{\frac{35}{2}} \text{Bff}(6,1)}{1716}-\frac{35 \sqrt{7} \text{Bff}(6,3)}{1144}-\frac{5}{104} \sqrt{\frac{105}{11}} \text{Bff}(6,5) $$ 0 $$ \frac{5}{52} \sqrt{\frac{21}{2}} \text{Bff}(6,1)+\frac{5}{104} \sqrt{\frac{35}{3}} \text{Bff}(6,3)+\frac{5}{104} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $
$ f_{\text{xyz}} $$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Bsf}(3,2) }$$ 0 $$ \sqrt{\frac{6}{35}} \text{Bpf}(2,1)-\frac{\text{Bpf}(4,1)}{3 \sqrt{7}}+\frac{1}{3} \text{Bpf}(4,3) $$ 0 $$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)+\frac{2}{11} \sqrt{\frac{10}{21}} \text{Adf}(5,1)+\frac{4}{33} \sqrt{5} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,2)-\frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,2)+\frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,4) }$$ 0 $$ \text{Aff}(0,0)-\frac{7}{33} \text{Aff}(4,0)-\frac{1}{33} \sqrt{70} \text{Aff}(4,4)+\frac{10}{143} \text{Aff}(6,0)-\frac{10}{143} \sqrt{14} \text{Aff}(6,4) $$ 0 $$ -\frac{2}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{\text{Bff}(4,1)}{22 \sqrt{3}}-\frac{1}{22} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{5}{429} \sqrt{\frac{35}{2}} \text{Bff}(6,1)-\frac{15}{286} \sqrt{7} \text{Bff}(6,3)+\frac{5}{26} \sqrt{\frac{35}{33}} \text{Bff}(6,5) $$ 0 $$ -\frac{7}{66} \sqrt{5} \text{Bff}(4,1)-\frac{1}{66} \sqrt{35} \text{Bff}(4,3)+\frac{5}{143} \sqrt{\frac{21}{2}} \text{Bff}(6,1)-\frac{5}{286} \sqrt{105} \text{Bff}(6,3)-\frac{5}{26} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $$ 0 $
$ f_{z\left(5x^2-r^2\right)} $$\color{darkred}{ 0 }$$ -\frac{9 \text{Apf}(2,0)}{10 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{3}{7}} \text{Apf}(2,2)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,0)+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Apf}(4,2) $$ 0 $$ -\frac{1}{5} \sqrt{\frac{3}{7}} \text{Bpf}(2,1)-\frac{1}{6} \sqrt{\frac{5}{14}} \text{Bpf}(4,1)+\frac{1}{6} \sqrt{\frac{5}{2}} \text{Bpf}(4,3) $$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{4 \text{Adf}(1,1)}{\sqrt{35}}-\frac{1}{2} \sqrt{\frac{3}{70}} \text{Adf}(3,1)-\frac{5 \text{Adf}(3,3)}{6 \sqrt{14}}+\frac{5}{11} \sqrt{\frac{3}{7}} \text{Adf}(5,1)-\frac{5}{33} \sqrt{2} \text{Adf}(5,3) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 \text{Bdf}(5,2)}{22 \sqrt{3}}-\frac{5}{22} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$ \frac{\text{Aff}(2,0)}{2 \sqrt{15}}+\frac{\text{Aff}(2,2)}{3 \sqrt{10}}+\frac{13}{88} \sqrt{\frac{5}{3}} \text{Aff}(4,0)+\frac{\text{Aff}(4,2)}{22 \sqrt{6}}-\frac{5}{44} \sqrt{\frac{7}{6}} \text{Aff}(4,4)+\frac{35}{572} \sqrt{\frac{5}{3}} \text{Aff}(6,0)-\frac{10}{429} \sqrt{7} \text{Aff}(6,2)-\frac{5}{286} \sqrt{\frac{105}{2}} \text{Aff}(6,4) $$ 0 $$ \text{Aff}(0,0)+\frac{1}{10} \text{Aff}(2,0)+\frac{\text{Aff}(2,2)}{\sqrt{6}}-\frac{17}{264} \text{Aff}(4,0)+\frac{1}{22} \sqrt{\frac{5}{2}} \text{Aff}(4,2)+\frac{5}{132} \sqrt{\frac{35}{2}} \text{Aff}(4,4)+\frac{75}{572} \text{Aff}(6,0)-\frac{10}{143} \sqrt{\frac{35}{3}} \text{Aff}(6,2)+\frac{25}{286} \sqrt{\frac{7}{2}} \text{Aff}(6,4) $$ 0 $$ \frac{2}{5} \sqrt{\frac{2}{3}} \text{Bff}(2,1)-\frac{1}{33} \sqrt{5} \text{Bff}(4,1)+\frac{1}{33} \sqrt{35} \text{Bff}(4,3)+\frac{25}{572} \sqrt{\frac{7}{6}} \text{Bff}(6,1)-\frac{15 \sqrt{105} \text{Bff}(6,3)}{1144}+\frac{25}{104} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $$ 0 $$ \frac{1}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{5 \text{Bff}(4,1)}{11 \sqrt{3}}-\frac{1}{11} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{35 \sqrt{\frac{35}{2}} \text{Bff}(6,1)}{1716}-\frac{5}{88} \sqrt{7} \text{Bff}(6,3)-\frac{5}{104} \sqrt{\frac{35}{33}} \text{Bff}(6,5) $
$ f_{x\left(5x^2-3r^2\right)} $$\color{darkred}{ \frac{1}{2} \sqrt{\frac{3}{7}} \text{Asf}(3,1)-\frac{1}{2} \sqrt{\frac{5}{7}} \text{Asf}(3,3) }$$ 0 $$ -\frac{3}{10} \sqrt{\frac{3}{7}} \text{Apf}(2,0)+\frac{9 \text{Apf}(2,2)}{5 \sqrt{14}}+\frac{\text{Apf}(4,0)}{2 \sqrt{21}}-\frac{1}{3} \sqrt{\frac{10}{21}} \text{Apf}(4,2)+\frac{1}{3} \sqrt{\frac{5}{6}} \text{Apf}(4,4) $$ 0 $$\color{darkred}{ \frac{2}{3} \sqrt{\frac{2}{7}} \text{Bdf}(3,2)+\frac{5 \text{Bdf}(5,2)}{33 \sqrt{2}}-\frac{5 \text{Bdf}(5,4)}{11 \sqrt{6}} }$$\color{darkred}{ 0 }$$\color{darkred}{ -3 \sqrt{\frac{2}{35}} \text{Adf}(1,1)+\frac{2 \text{Adf}(3,1)}{\sqrt{105}}-\frac{2 \text{Adf}(3,3)}{3 \sqrt{7}}-\frac{25 \text{Adf}(5,1)}{22 \sqrt{42}}+\frac{25}{132} \text{Adf}(5,3)-\frac{5}{44} \sqrt{5} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,1)-\frac{\text{Adf}(3,3)}{\sqrt{21}}-\frac{5}{66} \sqrt{\frac{7}{2}} \text{Adf}(5,1)+\frac{5 \text{Adf}(5,3)}{44 \sqrt{3}}+\frac{5}{44} \sqrt{\frac{5}{3}} \text{Adf}(5,5) }$$ 0 $$ -\frac{2}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{\text{Bff}(4,1)}{22 \sqrt{3}}-\frac{1}{22} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{5}{429} \sqrt{\frac{35}{2}} \text{Bff}(6,1)-\frac{15}{286} \sqrt{7} \text{Bff}(6,3)+\frac{5}{26} \sqrt{\frac{35}{33}} \text{Bff}(6,5) $$ 0 $$ \text{Aff}(0,0)-\frac{2}{15} \text{Aff}(2,0)+\frac{2}{5} \sqrt{\frac{2}{3}} \text{Aff}(2,2)+\frac{3}{44} \text{Aff}(4,0)-\frac{1}{11} \sqrt{\frac{5}{2}} \text{Aff}(4,2)+\frac{1}{22} \sqrt{\frac{35}{2}} \text{Aff}(4,4)-\frac{125 \text{Aff}(6,0)}{1716}+\frac{25}{572} \sqrt{\frac{35}{3}} \text{Aff}(6,2)-\frac{25}{286} \sqrt{\frac{7}{2}} \text{Aff}(6,4)+\frac{25}{52} \sqrt{\frac{7}{33}} \text{Aff}(6,6) $$ 0 $$ \frac{\text{Aff}(2,0)}{\sqrt{15}}+\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)-\frac{1}{44} \sqrt{\frac{5}{3}} \text{Aff}(4,0)+\frac{\text{Aff}(4,2)}{11 \sqrt{6}}+\frac{1}{22} \sqrt{\frac{7}{6}} \text{Aff}(4,4)-\frac{35}{572} \sqrt{\frac{5}{3}} \text{Aff}(6,0)+\frac{85 \sqrt{7} \text{Aff}(6,2)}{1716}-\frac{5}{286} \sqrt{\frac{35}{6}} \text{Aff}(6,4)-\frac{5}{52} \sqrt{\frac{35}{11}} \text{Aff}(6,6) $$ 0 $
$ f_{y\left(5x^2-r^2\right)} $$\color{darkred}{ 0 }$$ -\frac{1}{5} \sqrt{\frac{3}{7}} \text{Bpf}(2,1)-\frac{1}{6} \sqrt{\frac{5}{14}} \text{Bpf}(4,1)+\frac{1}{6} \sqrt{\frac{5}{2}} \text{Bpf}(4,3) $$ 0 $$ -\frac{3 \text{Apf}(2,0)}{10 \sqrt{14}}+\frac{1}{10} \sqrt{21} \text{Apf}(2,2)+\frac{\text{Apf}(4,0)}{6 \sqrt{14}}-\frac{1}{6} \sqrt{5} \text{Apf}(4,4) $$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{\text{Bdf}(3,2)}{\sqrt{21}}+\frac{5 \text{Bdf}(5,2)}{22 \sqrt{3}}-\frac{5}{22} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{4 \text{Adf}(1,1)}{\sqrt{35}}+\frac{1}{2} \sqrt{\frac{7}{30}} \text{Adf}(3,1)+\frac{\text{Adf}(3,3)}{6 \sqrt{14}}-\frac{5 \text{Adf}(5,1)}{22 \sqrt{21}}-\frac{5 \text{Adf}(5,3)}{66 \sqrt{2}}+\frac{5}{22} \sqrt{\frac{5}{2}} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$ -\frac{1}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{2 \text{Bff}(4,1)}{11 \sqrt{3}}+\frac{2}{11} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{25 \sqrt{\frac{35}{2}} \text{Bff}(6,1)}{1716}-\frac{35 \sqrt{7} \text{Bff}(6,3)}{1144}-\frac{5}{104} \sqrt{\frac{105}{11}} \text{Bff}(6,5) $$ 0 $$ \frac{2}{5} \sqrt{\frac{2}{3}} \text{Bff}(2,1)-\frac{1}{33} \sqrt{5} \text{Bff}(4,1)+\frac{1}{33} \sqrt{35} \text{Bff}(4,3)+\frac{25}{572} \sqrt{\frac{7}{6}} \text{Bff}(6,1)-\frac{15 \sqrt{105} \text{Bff}(6,3)}{1144}+\frac{25}{104} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $$ 0 $$ \text{Aff}(0,0)-\frac{3}{10} \text{Aff}(2,0)+\frac{\text{Aff}(2,2)}{5 \sqrt{6}}+\frac{23}{264} \text{Aff}(4,0)-\frac{5}{66} \sqrt{\frac{5}{2}} \text{Aff}(4,2)-\frac{1}{44} \sqrt{\frac{35}{2}} \text{Aff}(4,4)-\frac{25 \text{Aff}(6,0)}{1144}+\frac{5 \sqrt{\frac{35}{3}} \text{Aff}(6,2)}{1144}+\frac{25}{572} \sqrt{\frac{7}{2}} \text{Aff}(6,4)-\frac{25}{104} \sqrt{\frac{21}{11}} \text{Aff}(6,6) $$ 0 $$ \frac{\text{Aff}(2,0)}{2 \sqrt{15}}+\frac{\text{Aff}(2,2)}{3 \sqrt{10}}-\frac{1}{88} \sqrt{\frac{5}{3}} \text{Aff}(4,0)-\frac{13 \text{Aff}(4,2)}{22 \sqrt{6}}-\frac{7}{44} \sqrt{\frac{7}{6}} \text{Aff}(4,4)-\frac{35 \sqrt{\frac{5}{3}} \text{Aff}(6,0)}{1144}-\frac{5 \sqrt{7} \text{Aff}(6,2)}{3432}+\frac{35}{572} \sqrt{\frac{35}{6}} \text{Aff}(6,4)+\frac{5}{104} \sqrt{\frac{35}{11}} \text{Aff}(6,6) $
$ f_{x\left(y^2-z^2\right)} $$\color{darkred}{ \frac{1}{2} \sqrt{\frac{5}{7}} \text{Asf}(3,1)+\frac{1}{2} \sqrt{\frac{3}{7}} \text{Asf}(3,3) }$$ 0 $$ -\frac{3 \text{Apf}(2,0)}{2 \sqrt{35}}-\sqrt{\frac{3}{70}} \text{Apf}(2,2)+\frac{1}{6} \sqrt{\frac{5}{7}} \text{Apf}(4,0)-\frac{1}{3} \sqrt{\frac{2}{7}} \text{Apf}(4,2)-\frac{\text{Apf}(4,4)}{3 \sqrt{2}} $$ 0 $$\color{darkred}{ \frac{1}{11} \sqrt{\frac{15}{2}} \text{Bdf}(5,2)+\frac{1}{11} \sqrt{\frac{5}{2}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\frac{1}{22} \sqrt{\frac{35}{2}} \text{Adf}(5,1)+\frac{1}{44} \sqrt{15} \text{Adf}(5,3)+\frac{5}{44} \sqrt{3} \text{Adf}(5,5) }$$\color{darkred}{ 0 }$$\color{darkred}{ -\sqrt{\frac{2}{7}} \text{Adf}(1,1)-\frac{\text{Adf}(3,1)}{\sqrt{21}}+\frac{1}{3} \sqrt{\frac{5}{7}} \text{Adf}(3,3)-\frac{13}{22} \sqrt{\frac{5}{42}} \text{Adf}(5,1)-\frac{1}{12} \sqrt{5} \text{Adf}(5,3)-\frac{5}{44} \text{Adf}(5,5) }$$ 0 $$ -\frac{7}{66} \sqrt{5} \text{Bff}(4,1)-\frac{1}{66} \sqrt{35} \text{Bff}(4,3)+\frac{5}{143} \sqrt{\frac{21}{2}} \text{Bff}(6,1)-\frac{5}{286} \sqrt{105} \text{Bff}(6,3)-\frac{5}{26} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $$ 0 $$ \frac{\text{Aff}(2,0)}{\sqrt{15}}+\frac{1}{3} \sqrt{\frac{2}{5}} \text{Aff}(2,2)-\frac{1}{44} \sqrt{\frac{5}{3}} \text{Aff}(4,0)+\frac{\text{Aff}(4,2)}{11 \sqrt{6}}+\frac{1}{22} \sqrt{\frac{7}{6}} \text{Aff}(4,4)-\frac{35}{572} \sqrt{\frac{5}{3}} \text{Aff}(6,0)+\frac{85 \sqrt{7} \text{Aff}(6,2)}{1716}-\frac{5}{286} \sqrt{\frac{35}{6}} \text{Aff}(6,4)-\frac{5}{52} \sqrt{\frac{35}{11}} \text{Aff}(6,6) $$ 0 $$ \text{Aff}(0,0)+\frac{7}{132} \text{Aff}(4,0)+\frac{7}{33} \sqrt{\frac{5}{2}} \text{Aff}(4,2)-\frac{1}{22} \sqrt{\frac{35}{2}} \text{Aff}(4,4)-\frac{5}{44} \text{Aff}(6,0)+\frac{5}{572} \sqrt{105} \text{Aff}(6,2)+\frac{25}{286} \sqrt{\frac{7}{2}} \text{Aff}(6,4)+\frac{5}{52} \sqrt{\frac{21}{11}} \text{Aff}(6,6) $$ 0 $
$ f_{y\left(y^2-3z^2\right)} $$\color{darkred}{ 0 }$$ -\frac{3 \text{Bpf}(2,1)}{\sqrt{35}}-\frac{5 \text{Bpf}(4,1)}{2 \sqrt{42}}-\frac{\text{Bpf}(4,3)}{6 \sqrt{6}} $$ 0 $$ -\frac{3}{2} \sqrt{\frac{3}{70}} \text{Apf}(2,0)-\frac{3 \text{Apf}(2,2)}{2 \sqrt{35}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Apf}(4,0)+\frac{4 \text{Apf}(4,2)}{3 \sqrt{21}}+\frac{\text{Apf}(4,4)}{6 \sqrt{3}} $$\color{darkred}{ 0 }$$\color{darkred}{ \frac{1}{3} \sqrt{\frac{5}{7}} \text{Bdf}(3,2)+\frac{7}{66} \sqrt{5} \text{Bdf}(5,2)+\frac{1}{22} \sqrt{\frac{5}{3}} \text{Bdf}(5,4) }$$\color{darkred}{ 0 }$$\color{darkred}{ \frac{5 \text{Adf}(3,1)}{6 \sqrt{14}}+\frac{1}{2} \sqrt{\frac{5}{42}} \text{Adf}(3,3)-\frac{1}{66} \sqrt{35} \text{Adf}(5,1)-\frac{5}{22} \sqrt{\frac{5}{6}} \text{Adf}(5,3)-\frac{5 \text{Adf}(5,5)}{22 \sqrt{6}} }$$\color{darkred}{ 0 }$$ \frac{5}{52} \sqrt{\frac{21}{2}} \text{Bff}(6,1)+\frac{5}{104} \sqrt{\frac{35}{3}} \text{Bff}(6,3)+\frac{5}{104} \sqrt{\frac{7}{11}} \text{Bff}(6,5) $$ 0 $$ \frac{1}{3} \sqrt{\frac{2}{5}} \text{Bff}(2,1)+\frac{5 \text{Bff}(4,1)}{11 \sqrt{3}}-\frac{1}{11} \sqrt{\frac{7}{3}} \text{Bff}(4,3)+\frac{35 \sqrt{\frac{35}{2}} \text{Bff}(6,1)}{1716}-\frac{5}{88} \sqrt{7} \text{Bff}(6,3)-\frac{5}{104} \sqrt{\frac{35}{33}} \text{Bff}(6,5) $$ 0 $$ \frac{\text{Aff}(2,0)}{2 \sqrt{15}}+\frac{\text{Aff}(2,2)}{3 \sqrt{10}}-\frac{1}{88} \sqrt{\frac{5}{3}} \text{Aff}(4,0)-\frac{13 \text{Aff}(4,2)}{22 \sqrt{6}}-\frac{7}{44} \sqrt{\frac{7}{6}} \text{Aff}(4,4)-\frac{35 \sqrt{\frac{5}{3}} \text{Aff}(6,0)}{1144}-\frac{5 \sqrt{7} \text{Aff}(6,2)}{3432}+\frac{35}{572} \sqrt{\frac{35}{6}} \text{Aff}(6,4)+\frac{5}{104} \sqrt{\frac{35}{11}} \text{Aff}(6,6) $$ 0 $$ \text{Aff}(0,0)+\frac{1}{6} \text{Aff}(2,0)-\frac{\text{Aff}(2,2)}{\sqrt{6}}+\frac{3}{88} \text{Aff}(4,0)-\frac{1}{22} \sqrt{\frac{5}{2}} \text{Aff}(4,2)+\frac{1}{44} \sqrt{\frac{35}{2}} \text{Aff}(4,4)-\frac{565 \text{Aff}(6,0)}{3432}-\frac{85 \sqrt{\frac{35}{3}} \text{Aff}(6,2)}{1144}-\frac{25}{572} \sqrt{\frac{7}{2}} \text{Aff}(6,4)-\frac{5}{104} \sqrt{\frac{7}{33}} \text{Aff}(6,6) $

Coupling for a single shell

Although the parameters $A_{l'',l'}(k,m)$ uniquely define the potential, there is no simple relation between these paramters and the eigenstates of the potential. In this section we replace the parameters $A_{l'',l'}(k,m)$ by paramters that relate to the eigen energies of the potential acting on or between two shells with angular momentum $l''$ and $l'$.

Click on one of the subsections to expand it or

Potential for s orbitals

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} \text{Ea} & k=0\land m=0 \\ 0 & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{Ea, k == 0 && m == 0}}, 0]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{0, 0, Ea} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{0}^{(0)}} $
$ {Y_{0}^{(0)}} $$ \text{Ea} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ \text{s} $
$ \text{s} $$ \text{Ea} $

Rotation matrix used

Rotation matrix used

$ $ $ {Y_{0}^{(0)}} $
$ \text{s} $$ 1 $

Irriducible representations and their onsite energy

Irriducible representations and their onsite energy

$$\text{Ea}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2 \sqrt{\pi }}$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2 \sqrt{\pi }}$$

Potential for p orbitals

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} \frac{1}{3} (\text{Ea}+\text{Eby}+\text{Ebz}) & k=0\land m=0 \\ 0 & k\neq 2\lor (m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2) \\ \frac{5 (\text{Ea}-\text{Eby})}{2 \sqrt{6}} & k=2\land (m=-2\lor m=2) \\ \frac{5 i \text{Mb}}{\sqrt{6}} & k=2\land (m=-1\lor m=1) \\ -\frac{5}{6} (\text{Ea}+\text{Eby}-2 \text{Ebz}) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{(Ea + Eby + Ebz)/3, k == 0 && m == 0}, {0, k != 2 || (m != -2 && m != -1 && m != 0 && m != 1 && m != 2)}, {(5*(Ea - Eby))/(2*Sqrt[6]), k == 2 && (m == -2 || m == 2)}, {((5*I)*Mb)/Sqrt[6], k == 2 && (m == -1 || m == 1)}}, (-5*(Ea + Eby - 2*Ebz))/6]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{0, 0, (1/3)*(Ea + Eby + Ebz)} , 
       {2, 0, (-5/6)*(Ea + Eby + (-2)*(Ebz))} , 
       {2,-1, (5*I)*((1/(sqrt(6)))*(Mb))} , 
       {2, 1, (5*I)*((1/(sqrt(6)))*(Mb))} , 
       {2,-2, (5/2)*((1/(sqrt(6)))*(Ea + (-1)*(Eby)))} , 
       {2, 2, (5/2)*((1/(sqrt(6)))*(Ea + (-1)*(Eby)))} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-1}^{(1)}} $ $ {Y_{0}^{(1)}} $ $ {Y_{1}^{(1)}} $
$ {Y_{-1}^{(1)}} $$ \frac{\text{Ea}+\text{Eby}}{2} $$ \frac{i \text{Mb}}{\sqrt{2}} $$ \frac{\text{Eby}-\text{Ea}}{2} $
$ {Y_{0}^{(1)}} $$ -\frac{i \text{Mb}}{\sqrt{2}} $$ \text{Ebz} $$ -\frac{i \text{Mb}}{\sqrt{2}} $
$ {Y_{1}^{(1)}} $$ \frac{\text{Eby}-\text{Ea}}{2} $$ \frac{i \text{Mb}}{\sqrt{2}} $$ \frac{\text{Ea}+\text{Eby}}{2} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ p_z $ $ p_x $ $ p_y $
$ p_z $$ \text{Ebz} $$ 0 $$ \text{Mb} $
$ p_x $$ 0 $$ \text{Ea} $$ 0 $
$ p_y $$ \text{Mb} $$ 0 $$ \text{Eby} $

Rotation matrix used

Rotation matrix used

$ $ $ {Y_{-1}^{(1)}} $ $ {Y_{0}^{(1)}} $ $ {Y_{1}^{(1)}} $
$ p_z $$ 0 $$ 1 $$ 0 $
$ p_x $$ \frac{1}{\sqrt{2}} $$ 0 $$ -\frac{1}{\sqrt{2}} $
$ p_y $$ \frac{i}{\sqrt{2}} $$ 0 $$ \frac{i}{\sqrt{2}} $

Irriducible representations and their onsite energy

Irriducible representations and their onsite energy

$$\text{Ebz}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} \cos (\theta )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} z$$
$$\text{Ea}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} \sin (\theta ) \cos (\phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} x$$
$$\text{Eby}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} \sin (\theta ) \sin (\phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{3}{\pi }} y$$

Potential for d orbitals

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} \frac{1}{5} (\text{Eax2}+\text{Eay2z2}+\text{Eayz}+\text{Ebxy}+\text{Ebxz}) & k=0\land m=0 \\ 0 & (k\neq 2\land k\neq 4)\lor (k\neq 4\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2)\lor (m\neq -4\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2\land m\neq 3\land m\neq 4) \\ \frac{1}{4} \left(\sqrt{6} \text{Eax2}-\sqrt{6} \text{Eay2z2}-\sqrt{6} \text{Eayz}+\sqrt{6} \text{Ebxz}+2 \sqrt{2} \text{May2z2x2}\right) & k=2\land (m=-2\lor m=2) \\ \frac{1}{2} i \left(\sqrt{6} \text{Mb}-2 \sqrt{2} \text{Max2yz}\right) & k=2\land (m=-1\lor m=1) \\ \frac{1}{2} \left(-\text{Eax2}+\text{Eay2z2}+\text{Eayz}-2 \text{Ebxy}+\text{Ebxz}+2 \sqrt{3} \text{May2z2x2}\right) & k=2\land m=0 \\ \frac{3}{8} \sqrt{\frac{7}{10}} \left(3 \text{Eax2}+\text{Eay2z2}-4 \text{Ebxy}-2 \sqrt{3} \text{May2z2x2}\right) & k=4\land (m=-4\lor m=4) \\ \frac{3}{4} i \sqrt{\frac{7}{5}} \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}+2 \text{Mb}\right) & k=4\land (m=-3\lor m=3) \\ -\frac{3 \left(3 \text{Eax2}-3 \text{Eay2z2}+4 \text{Eayz}-4 \text{Ebxz}+2 \sqrt{3} \text{May2z2x2}\right)}{4 \sqrt{10}} & k=4\land (m=-2\lor m=2) \\ -\frac{3 i \left(\sqrt{3} \text{Max2yz}+7 \text{May2z2yz}+2 \text{Mb}\right)}{4 \sqrt{5}} & k=4\land (m=-1\lor m=1) \\ \frac{3}{40} \left(9 \text{Eax2}+19 \text{Eay2z2}+2 \left(-8 \text{Eayz}+2 \text{Ebxy}-8 \text{Ebxz}+5 \sqrt{3} \text{May2z2x2}\right)\right) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{(Eax2 + Eay2z2 + Eayz + Ebxy + Ebxz)/5, k == 0 && m == 0}, {0, (k != 2 && k != 4) || (k != 4 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2) || (m != -4 && m != -3 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2 && m != 3 && m != 4)}, {(Sqrt[6]*Eax2 - Sqrt[6]*Eay2z2 - Sqrt[6]*Eayz + Sqrt[6]*Ebxz + 2*Sqrt[2]*May2z2x2)/4, k == 2 && (m == -2 || m == 2)}, {(I/2)*(-2*Sqrt[2]*Max2yz + Sqrt[6]*Mb), k == 2 && (m == -1 || m == 1)}, {(-Eax2 + Eay2z2 + Eayz - 2*Ebxy + Ebxz + 2*Sqrt[3]*May2z2x2)/2, k == 2 && m == 0}, {(3*Sqrt[7/10]*(3*Eax2 + Eay2z2 - 4*Ebxy - 2*Sqrt[3]*May2z2x2))/8, k == 4 && (m == -4 || m == 4)}, {((3*I)/4)*Sqrt[7/5]*(Sqrt[3]*Max2yz - May2z2yz + 2*Mb), k == 4 && (m == -3 || m == 3)}, {(-3*(3*Eax2 - 3*Eay2z2 + 4*Eayz - 4*Ebxz + 2*Sqrt[3]*May2z2x2))/(4*Sqrt[10]), k == 4 && (m == -2 || m == 2)}, {(((-3*I)/4)*(Sqrt[3]*Max2yz + 7*May2z2yz + 2*Mb))/Sqrt[5], k == 4 && (m == -1 || m == 1)}}, (3*(9*Eax2 + 19*Eay2z2 + 2*(-8*Eayz + 2*Ebxy - 8*Ebxz + 5*Sqrt[3]*May2z2x2)))/40]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{0, 0, (1/5)*(Eax2 + Eay2z2 + Eayz + Ebxy + Ebxz)} , 
       {2, 0, (1/2)*((-1)*(Eax2) + Eay2z2 + Eayz + (-2)*(Ebxy) + Ebxz + (2)*((sqrt(3))*(May2z2x2)))} , 
       {2,-1, (1/2*I)*((-2)*((sqrt(2))*(Max2yz)) + (sqrt(6))*(Mb))} , 
       {2, 1, (1/2*I)*((-2)*((sqrt(2))*(Max2yz)) + (sqrt(6))*(Mb))} , 
       {2,-2, (1/4)*((sqrt(6))*(Eax2) + (-1)*((sqrt(6))*(Eay2z2)) + (-1)*((sqrt(6))*(Eayz)) + (sqrt(6))*(Ebxz) + (2)*((sqrt(2))*(May2z2x2)))} , 
       {2, 2, (1/4)*((sqrt(6))*(Eax2) + (-1)*((sqrt(6))*(Eay2z2)) + (-1)*((sqrt(6))*(Eayz)) + (sqrt(6))*(Ebxz) + (2)*((sqrt(2))*(May2z2x2)))} , 
       {4, 0, (3/40)*((9)*(Eax2) + (19)*(Eay2z2) + (2)*((-8)*(Eayz) + (2)*(Ebxy) + (-8)*(Ebxz) + (5)*((sqrt(3))*(May2z2x2))))} , 
       {4,-1, (-3/4*I)*((1/(sqrt(5)))*((sqrt(3))*(Max2yz) + (7)*(May2z2yz) + (2)*(Mb)))} , 
       {4, 1, (-3/4*I)*((1/(sqrt(5)))*((sqrt(3))*(Max2yz) + (7)*(May2z2yz) + (2)*(Mb)))} , 
       {4,-2, (-3/4)*((1/(sqrt(10)))*((3)*(Eax2) + (-3)*(Eay2z2) + (4)*(Eayz) + (-4)*(Ebxz) + (2)*((sqrt(3))*(May2z2x2))))} , 
       {4, 2, (-3/4)*((1/(sqrt(10)))*((3)*(Eax2) + (-3)*(Eay2z2) + (4)*(Eayz) + (-4)*(Ebxz) + (2)*((sqrt(3))*(May2z2x2))))} , 
       {4,-3, (3/4*I)*((sqrt(7/5))*((sqrt(3))*(Max2yz) + (-1)*(May2z2yz) + (2)*(Mb)))} , 
       {4, 3, (3/4*I)*((sqrt(7/5))*((sqrt(3))*(Max2yz) + (-1)*(May2z2yz) + (2)*(Mb)))} , 
       {4,-4, (3/8)*((sqrt(7/10))*((3)*(Eax2) + Eay2z2 + (-4)*(Ebxy) + (-2)*((sqrt(3))*(May2z2x2))))} , 
       {4, 4, (3/8)*((sqrt(7/10))*((3)*(Eax2) + Eay2z2 + (-4)*(Ebxy) + (-2)*((sqrt(3))*(May2z2x2))))} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $
$ {Y_{-2}^{(2)}} $$ \frac{1}{8} \left(3 \text{Eax2}+\text{Eay2z2}+4 \text{Ebxy}-2 \sqrt{3} \text{May2z2x2}\right) $$ -\frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}-2 \text{Mb}\right) $$ \frac{1}{8} \left(-\sqrt{6} \text{Eax2}+\sqrt{6} \text{Eay2z2}-2 \sqrt{2} \text{May2z2x2}\right) $$ -\frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}+2 \text{Mb}\right) $$ \frac{1}{8} \left(3 \text{Eax2}+\text{Eay2z2}-4 \text{Ebxy}-2 \sqrt{3} \text{May2z2x2}\right) $
$ {Y_{-1}^{(2)}} $$ \frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}-2 \text{Mb}\right) $$ \frac{\text{Eayz}+\text{Ebxz}}{2} $$ -\frac{i \left(\text{Max2yz}+\sqrt{3} \text{May2z2yz}\right)}{2 \sqrt{2}} $$ \frac{\text{Eayz}-\text{Ebxz}}{2} $$ \frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}+2 \text{Mb}\right) $
$ {Y_{0}^{(2)}} $$ \frac{1}{8} \left(-\sqrt{6} \text{Eax2}+\sqrt{6} \text{Eay2z2}-2 \sqrt{2} \text{May2z2x2}\right) $$ \frac{i \left(\text{Max2yz}+\sqrt{3} \text{May2z2yz}\right)}{2 \sqrt{2}} $$ \frac{1}{4} \left(\text{Eax2}+3 \text{Eay2z2}+2 \sqrt{3} \text{May2z2x2}\right) $$ \frac{i \left(\text{Max2yz}+\sqrt{3} \text{May2z2yz}\right)}{2 \sqrt{2}} $$ \frac{1}{8} \left(-\sqrt{6} \text{Eax2}+\sqrt{6} \text{Eay2z2}-2 \sqrt{2} \text{May2z2x2}\right) $
$ {Y_{1}^{(2)}} $$ \frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}+2 \text{Mb}\right) $$ \frac{\text{Eayz}-\text{Ebxz}}{2} $$ -\frac{i \left(\text{Max2yz}+\sqrt{3} \text{May2z2yz}\right)}{2 \sqrt{2}} $$ \frac{\text{Eayz}+\text{Ebxz}}{2} $$ \frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}-2 \text{Mb}\right) $
$ {Y_{2}^{(2)}} $$ \frac{1}{8} \left(3 \text{Eax2}+\text{Eay2z2}-4 \text{Ebxy}-2 \sqrt{3} \text{May2z2x2}\right) $$ -\frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}+2 \text{Mb}\right) $$ \frac{1}{8} \left(-\sqrt{6} \text{Eax2}+\sqrt{6} \text{Eay2z2}-2 \sqrt{2} \text{May2z2x2}\right) $$ -\frac{1}{4} i \left(\sqrt{3} \text{Max2yz}-\text{May2z2yz}-2 \text{Mb}\right) $$ \frac{1}{8} \left(3 \text{Eax2}+\text{Eay2z2}+4 \text{Ebxy}-2 \sqrt{3} \text{May2z2x2}\right) $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ d_{\text{yz}} $ $ d_{\text{xz}} $ $ d_{3x^2-r^2} $ $ d_{\text{xz}} $ $ d_{y^2-z^2} $
$ d_{\text{yz}} $$ \text{Eayz} $$ 0 $$ \text{Max2yz} $$ 0 $$ \text{May2z2yz} $
$ d_{\text{xz}} $$ 0 $$ \text{Ebxz} $$ 0 $$ \text{Mb} $$ 0 $
$ d_{3x^2-r^2} $$ \text{Max2yz} $$ 0 $$ \text{Eax2} $$ 0 $$ \text{May2z2x2} $
$ d_{\text{xz}} $$ 0 $$ \text{Mb} $$ 0 $$ \text{Ebxy} $$ 0 $
$ d_{y^2-z^2} $$ \text{May2z2yz} $$ 0 $$ \text{May2z2x2} $$ 0 $$ \text{Eay2z2} $

Rotation matrix used

Rotation matrix used

$ $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $
$ d_{\text{yz}} $$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $
$ d_{\text{xz}} $$ 0 $$ \frac{1}{\sqrt{2}} $$ 0 $$ -\frac{1}{\sqrt{2}} $$ 0 $
$ d_{3x^2-r^2} $$ \frac{\sqrt{\frac{3}{2}}}{2} $$ 0 $$ -\frac{1}{2} $$ 0 $$ \frac{\sqrt{\frac{3}{2}}}{2} $
$ d_{\text{xz}} $$ \frac{i}{\sqrt{2}} $$ 0 $$ 0 $$ 0 $$ -\frac{i}{\sqrt{2}} $
$ d_{y^2-z^2} $$ -\frac{1}{2 \sqrt{2}} $$ 0 $$ -\frac{\sqrt{3}}{2} $$ 0 $$ -\frac{1}{2 \sqrt{2}} $

Irriducible representations and their onsite energy

Irriducible representations and their onsite energy

$$\text{Eayz}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{4} \sqrt{\frac{15}{\pi }} \sin (2 \theta ) \sin (\phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{15}{\pi }} y z$$
$$\text{Ebxz}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{4} \sqrt{\frac{15}{\pi }} \sin (2 \theta ) \cos (\phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{15}{\pi }} x z$$
$$\text{Eax2}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{5}{\pi }} \left(-6 \sin ^2(\theta ) \cos (2 \phi )+3 \cos (2 \theta )+1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{8} \sqrt{\frac{5}{\pi }} \left(3 x^2-3 y^2-3 z^2+1\right)$$
$$\text{Ebxy}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{4} \sqrt{\frac{15}{\pi }} \sin ^2(\theta ) \sin (2 \phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{15}{\pi }} x y$$
$$\text{Eay2z2}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{15}{\pi }} \left(2 \sin ^2(\theta ) \cos (2 \phi )+3 \cos (2 \theta )+1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{8} \sqrt{\frac{15}{\pi }} \left(-x^2+y^2-3 z^2+1\right)$$

Potential for f orbitals

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} A(0,0) & k=0\land m=0 \\ 0 & (k\neq 2\land k\neq 4\land k\neq 6)\lor (k\neq 4\land k\neq 6\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2)\lor (k\neq 6\land m\neq -4\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2\land m\neq 3\land m\neq 4)\lor (m\neq -6\land m\neq -5\land m\neq -4\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2\land m\neq 3\land m\neq 4\land m\neq 5\land m\neq 6) \\ A(2,2) & k=2\land (m=-2\lor m=2) \\ i B(2,1) & k=2\land (m=-1\lor m=1) \\ A(2,0) & k=2\land m=0 \\ A(4,4) & k=4\land (m=-4\lor m=4) \\ i B(4,3) & k=4\land (m=-3\lor m=3) \\ A(4,2) & k=4\land (m=-2\lor m=2) \\ i B(4,1) & k=4\land (m=-1\lor m=1) \\ A(4,0) & k=4\land m=0 \\ A(6,6) & k=6\land (m=-6\lor m=6) \\ i B(6,5) & k=6\land (m=-5\lor m=5) \\ A(6,4) & k=6\land (m=-4\lor m=4) \\ i B(6,3) & k=6\land (m=-3\lor m=3) \\ A(6,2) & k=6\land (m=-2\lor m=2) \\ i B(6,1) & k=6\land (m=-1\lor m=1) \\ A(6,0) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{A[0, 0], k == 0 && m == 0}, {0, (k != 2 && k != 4 && k != 6) || (k != 4 && k != 6 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2) || (k != 6 && m != -4 && m != -3 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2 && m != 3 && m != 4) || (m != -6 && m != -5 && m != -4 && m != -3 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2 && m != 3 && m != 4 && m != 5 && m != 6)}, {A[2, 2], k == 2 && (m == -2 || m == 2)}, {I*B[2, 1], k == 2 && (m == -1 || m == 1)}, {A[2, 0], k == 2 && m == 0}, {A[4, 4], k == 4 && (m == -4 || m == 4)}, {I*B[4, 3], k == 4 && (m == -3 || m == 3)}, {A[4, 2], k == 4 && (m == -2 || m == 2)}, {I*B[4, 1], k == 4 && (m == -1 || m == 1)}, {A[4, 0], k == 4 && m == 0}, {A[6, 6], k == 6 && (m == -6 || m == 6)}, {I*B[6, 5], k == 6 && (m == -5 || m == 5)}, {A[6, 4], k == 6 && (m == -4 || m == 4)}, {I*B[6, 3], k == 6 && (m == -3 || m == 3)}, {A[6, 2], k == 6 && (m == -2 || m == 2)}, {I*B[6, 1], k == 6 && (m == -1 || m == 1)}}, A[6, 0]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{0, 0, A(0,0)} , 
       {2, 0, A(2,0)} , 
       {2,-1, (I)*(B(2,1))} , 
       {2, 1, (I)*(B(2,1))} , 
       {2,-2, A(2,2)} , 
       {2, 2, A(2,2)} , 
       {4, 0, A(4,0)} , 
       {4,-1, (I)*(B(4,1))} , 
       {4, 1, (I)*(B(4,1))} , 
       {4,-2, A(4,2)} , 
       {4, 2, A(4,2)} , 
       {4,-3, (I)*(B(4,3))} , 
       {4, 3, (I)*(B(4,3))} , 
       {4,-4, A(4,4)} , 
       {4, 4, A(4,4)} , 
       {6, 0, A(6,0)} , 
       {6,-1, (I)*(B(6,1))} , 
       {6, 1, (I)*(B(6,1))} , 
       {6,-2, A(6,2)} , 
       {6, 2, A(6,2)} , 
       {6,-3, (I)*(B(6,3))} , 
       {6, 3, (I)*(B(6,3))} , 
       {6,-4, A(6,4)} , 
       {6, 4, A(6,4)} , 
       {6,-5, (I)*(B(6,5))} , 
       {6, 5, (I)*(B(6,5))} , 
       {6,-6, A(6,6)} , 
       {6, 6, A(6,6)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ {Y_{-3}^{(3)}} $$ A(0,0)-\frac{1}{3} A(2,0)+\frac{1}{11} A(4,0)-\frac{5}{429} A(6,0) $$ \frac{1}{429} i \left(143 B(2,1)-13 \sqrt{30} B(4,1)+5 \sqrt{7} B(6,1)\right) $$ -\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{1}{11} \sqrt{6} A(4,2)-\frac{10}{429} \sqrt{7} A(6,2) $$ -\frac{1}{429} i \sqrt{7} \left(39 B(4,3)-10 \sqrt{3} B(6,3)\right) $$ \frac{1}{143} \sqrt{\frac{14}{3}} \left(13 A(4,4)-5 \sqrt{5} A(6,4)\right) $$ \frac{5}{13} i \sqrt{\frac{14}{33}} B(6,5) $$ -\frac{10}{13} \sqrt{\frac{7}{33}} A(6,6) $
$ {Y_{-2}^{(3)}} $$ -\frac{1}{429} i \left(143 B(2,1)-13 \sqrt{30} B(4,1)+5 \sqrt{7} B(6,1)\right) $$ A(0,0)-\frac{7}{33} A(4,0)+\frac{10}{143} A(6,0) $$ \frac{i B(2,1)}{\sqrt{15}}+\frac{1}{429} i \left(52 \sqrt{2} B(4,1)-5 \sqrt{105} B(6,1)\right) $$ \frac{-286 \sqrt{5} A(2,2)-65 \sqrt{3} A(4,2)+100 \sqrt{14} A(6,2)}{2145} $$ -\frac{1}{429} i \sqrt{14} \left(13 B(4,3)+15 \sqrt{3} B(6,3)\right) $$ \frac{1}{429} \sqrt{14} \left(13 \sqrt{5} A(4,4)+30 A(6,4)\right) $$ -\frac{5}{13} i \sqrt{\frac{14}{33}} B(6,5) $
$ {Y_{-1}^{(3)}} $$ -\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{1}{11} \sqrt{6} A(4,2)-\frac{10}{429} \sqrt{7} A(6,2) $$ -\frac{i \left(143 \sqrt{15} B(2,1)+260 \sqrt{2} B(4,1)-25 \sqrt{105} B(6,1)\right)}{2145} $$ A(0,0)+\frac{1}{5} A(2,0)+\frac{1}{33} A(4,0)-\frac{25}{143} A(6,0) $$ \frac{i \left(143 \sqrt{2} B(2,1)+65 \sqrt{15} B(4,1)+125 \sqrt{14} B(6,1)\right)}{2145} $$ -\frac{2 \left(143 \sqrt{6} A(2,2)+65 \sqrt{10} A(4,2)+25 \sqrt{105} A(6,2)\right)}{2145} $$ \frac{1}{429} i \sqrt{14} \left(13 B(4,3)+15 \sqrt{3} B(6,3)\right) $$ \frac{1}{143} \sqrt{\frac{14}{3}} \left(13 A(4,4)-5 \sqrt{5} A(6,4)\right) $
$ {Y_{0}^{(3)}} $$ \frac{1}{429} i \sqrt{7} \left(39 B(4,3)-10 \sqrt{3} B(6,3)\right) $$ \frac{-286 \sqrt{5} A(2,2)-65 \sqrt{3} A(4,2)+100 \sqrt{14} A(6,2)}{2145} $$ -\frac{i \left(143 \sqrt{2} B(2,1)+65 \sqrt{15} B(4,1)+125 \sqrt{14} B(6,1)\right)}{2145} $$ A(0,0)+\frac{4}{15} A(2,0)+\frac{2}{429} (39 A(4,0)+50 A(6,0)) $$ -\frac{i \left(143 \sqrt{2} B(2,1)+65 \sqrt{15} B(4,1)+125 \sqrt{14} B(6,1)\right)}{2145} $$ \frac{-286 \sqrt{5} A(2,2)-65 \sqrt{3} A(4,2)+100 \sqrt{14} A(6,2)}{2145} $$ \frac{1}{429} i \sqrt{7} \left(39 B(4,3)-10 \sqrt{3} B(6,3)\right) $
$ {Y_{1}^{(3)}} $$ \frac{1}{143} \sqrt{\frac{14}{3}} \left(13 A(4,4)-5 \sqrt{5} A(6,4)\right) $$ \frac{1}{429} i \sqrt{14} \left(13 B(4,3)+15 \sqrt{3} B(6,3)\right) $$ -\frac{2 \left(143 \sqrt{6} A(2,2)+65 \sqrt{10} A(4,2)+25 \sqrt{105} A(6,2)\right)}{2145} $$ \frac{i \left(143 \sqrt{2} B(2,1)+65 \sqrt{15} B(4,1)+125 \sqrt{14} B(6,1)\right)}{2145} $$ A(0,0)+\frac{1}{5} A(2,0)+\frac{1}{33} A(4,0)-\frac{25}{143} A(6,0) $$ -\frac{i \left(143 \sqrt{15} B(2,1)+260 \sqrt{2} B(4,1)-25 \sqrt{105} B(6,1)\right)}{2145} $$ -\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{1}{11} \sqrt{6} A(4,2)-\frac{10}{429} \sqrt{7} A(6,2) $
$ {Y_{2}^{(3)}} $$ -\frac{5}{13} i \sqrt{\frac{14}{33}} B(6,5) $$ \frac{1}{429} \sqrt{14} \left(13 \sqrt{5} A(4,4)+30 A(6,4)\right) $$ -\frac{1}{429} i \sqrt{14} \left(13 B(4,3)+15 \sqrt{3} B(6,3)\right) $$ \frac{-286 \sqrt{5} A(2,2)-65 \sqrt{3} A(4,2)+100 \sqrt{14} A(6,2)}{2145} $$ \frac{i B(2,1)}{\sqrt{15}}+\frac{1}{429} i \left(52 \sqrt{2} B(4,1)-5 \sqrt{105} B(6,1)\right) $$ A(0,0)-\frac{7}{33} A(4,0)+\frac{10}{143} A(6,0) $$ -\frac{1}{429} i \left(143 B(2,1)-13 \sqrt{30} B(4,1)+5 \sqrt{7} B(6,1)\right) $
$ {Y_{3}^{(3)}} $$ -\frac{10}{13} \sqrt{\frac{7}{33}} A(6,6) $$ \frac{5}{13} i \sqrt{\frac{14}{33}} B(6,5) $$ \frac{1}{143} \sqrt{\frac{14}{3}} \left(13 A(4,4)-5 \sqrt{5} A(6,4)\right) $$ -\frac{1}{429} i \sqrt{7} \left(39 B(4,3)-10 \sqrt{3} B(6,3)\right) $$ -\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{1}{11} \sqrt{6} A(4,2)-\frac{10}{429} \sqrt{7} A(6,2) $$ \frac{1}{429} i \left(143 B(2,1)-13 \sqrt{30} B(4,1)+5 \sqrt{7} B(6,1)\right) $$ A(0,0)-\frac{1}{3} A(2,0)+\frac{1}{11} A(4,0)-\frac{5}{429} A(6,0) $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ f_{z\left(3y^2-z^2\right)} $ $ f_{\text{xyz}} $ $ f_{z\left(5x^2-r^2\right)} $ $ f_{x\left(5x^2-3r^2\right)} $ $ f_{y\left(5x^2-r^2\right)} $ $ f_{x\left(y^2-z^2\right)} $ $ f_{y\left(y^2-3z^2\right)} $
$ f_{z\left(3y^2-z^2\right)} $$ \frac{3432 A(0,0)+572 A(2,0)-572 \sqrt{6} A(2,2)+117 A(4,0)-78 \sqrt{10} A(4,2)+39 \sqrt{70} A(4,4)+590 A(6,0)+80 \sqrt{105} A(6,2)+90 \sqrt{14} A(6,4)}{3432} $$ 0 $$ \frac{A(2,0)}{2 \sqrt{15}}+\frac{A(2,2)}{3 \sqrt{10}}+\frac{169 \sqrt{15} A(4,0)+26 \sqrt{6} A(4,2)-65 \sqrt{42} A(4,4)+70 \sqrt{15} A(6,0)-80 \sqrt{7} A(6,2)-30 \sqrt{210} A(6,4)}{3432} $$ 0 $$ -\frac{1}{3} \sqrt{\frac{2}{5}} B(2,1)+\frac{2 B(4,1)}{11 \sqrt{3}}+\frac{\sqrt{7} \left(208 \sqrt{3} B(4,3)+25 \sqrt{10} B(6,1)-15 \left(7 B(6,3)+\sqrt{165} B(6,5)\right)\right)}{3432} $$ 0 $$ \frac{5 \left(66 \sqrt{21} B(6,1)+11 \sqrt{210} B(6,3)+3 \sqrt{154} B(6,5)\right)}{3432 \sqrt{2}} $
$ f_{\text{xyz}} $$ 0 $$ \frac{1}{429} \left(429 A(0,0)-91 A(4,0)-13 \sqrt{70} A(4,4)+30 A(6,0)-30 \sqrt{14} A(6,4)\right) $$ 0 $$ \frac{-572 \sqrt{10} B(2,1)+65 \sqrt{3} B(4,1)+5 \sqrt{7} \left(-13 \sqrt{3} B(4,3)+5 \sqrt{10} B(6,1)-45 B(6,3)+5 \sqrt{165} B(6,5)\right)}{4290} $$ 0 $$ \frac{1}{858} \left(-91 \sqrt{5} B(4,1)-13 \sqrt{35} B(4,3)+15 \left(\sqrt{42} B(6,1)-\sqrt{105} B(6,3)-\sqrt{77} B(6,5)\right)\right) $$ 0 $
$ f_{z\left(5x^2-r^2\right)} $$ \frac{A(2,0)}{2 \sqrt{15}}+\frac{A(2,2)}{3 \sqrt{10}}+\frac{169 \sqrt{15} A(4,0)+26 \sqrt{6} A(4,2)-65 \sqrt{42} A(4,4)+70 \sqrt{15} A(6,0)-80 \sqrt{7} A(6,2)-30 \sqrt{210} A(6,4)}{3432} $$ 0 $$ A(0,0)+\frac{1}{10} A(2,0)+\frac{572 \sqrt{6} A(2,2)-221 A(4,0)+78 \sqrt{10} A(4,2)+65 \sqrt{70} A(4,4)+450 A(6,0)-80 \sqrt{105} A(6,2)+150 \sqrt{14} A(6,4)}{3432} $$ 0 $$ \frac{2}{5} \sqrt{\frac{2}{3}} B(2,1)+\frac{-104 \sqrt{5} B(4,1)+104 \sqrt{35} B(4,3)+25 \sqrt{42} B(6,1)-45 \sqrt{105} B(6,3)+75 \sqrt{77} B(6,5)}{3432} $$ 0 $$ \frac{1}{3} \sqrt{\frac{2}{5}} B(2,1)+\frac{5 B(4,1)}{11 \sqrt{3}}-\frac{\sqrt{7} \left(104 \sqrt{3} B(4,3)+5 \left(-7 \sqrt{10} B(6,1)+39 B(6,3)+\sqrt{165} B(6,5)\right)\right)}{3432} $
$ f_{x\left(5x^2-3r^2\right)} $$ 0 $$ \frac{-1144 \sqrt{5} B(2,1)+65 \sqrt{6} B(4,1)-65 \sqrt{42} B(4,3)+50 \sqrt{35} B(6,1)-225 \sqrt{14} B(6,3)+25 \sqrt{2310} B(6,5)}{4290 \sqrt{2}} $$ 0 $$ \frac{8580 A(0,0)-1144 A(2,0)+1144 \sqrt{6} A(2,2)+585 A(4,0)-390 \sqrt{10} A(4,2)+195 \sqrt{70} A(4,4)-625 A(6,0)+125 \sqrt{105} A(6,2)-375 \sqrt{14} A(6,4)+125 \sqrt{231} A(6,6)}{8580} $$ 0 $$ \frac{A(2,0)}{\sqrt{15}}+\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{-13 \sqrt{15} A(4,0)+26 \sqrt{6} A(4,2)+13 \sqrt{42} A(4,4)-35 \sqrt{15} A(6,0)+85 \sqrt{7} A(6,2)-5 \sqrt{210} A(6,4)-15 \sqrt{385} A(6,6)}{1716} $$ 0 $
$ f_{y\left(5x^2-r^2\right)} $$ -\frac{1}{3} \sqrt{\frac{2}{5}} B(2,1)+\frac{2 B(4,1)}{11 \sqrt{3}}+\frac{\sqrt{7} \left(208 \sqrt{3} B(4,3)+25 \sqrt{10} B(6,1)-15 \left(7 B(6,3)+\sqrt{165} B(6,5)\right)\right)}{3432} $$ 0 $$ \frac{2}{5} \sqrt{\frac{2}{3}} B(2,1)+\frac{-104 \sqrt{5} B(4,1)+104 \sqrt{35} B(4,3)+25 \sqrt{42} B(6,1)-45 \sqrt{105} B(6,3)+75 \sqrt{77} B(6,5)}{3432} $$ 0 $$ \frac{17160 A(0,0)-5148 A(2,0)+572 \sqrt{6} A(2,2)+1495 A(4,0)-650 \sqrt{10} A(4,2)-195 \sqrt{70} A(4,4)-375 A(6,0)+25 \sqrt{105} A(6,2)+375 \sqrt{14} A(6,4)-375 \sqrt{231} A(6,6)}{17160} $$ 0 $$ \frac{572 \sqrt{15} A(2,0)+572 \sqrt{10} A(2,2)-5 \left(13 \sqrt{15} A(4,0)+338 \sqrt{6} A(4,2)+91 \sqrt{42} A(4,4)+35 \sqrt{15} A(6,0)+5 \sqrt{7} A(6,2)-35 \sqrt{210} A(6,4)-15 \sqrt{385} A(6,6)\right)}{17160} $
$ f_{x\left(y^2-z^2\right)} $$ 0 $$ -\frac{91 \sqrt{10} B(4,1)+13 \sqrt{70} B(4,3)-30 \sqrt{21} B(6,1)+15 \sqrt{210} B(6,3)+15 \sqrt{154} B(6,5)}{858 \sqrt{2}} $$ 0 $$ \frac{A(2,0)}{\sqrt{15}}+\frac{1}{3} \sqrt{\frac{2}{5}} A(2,2)+\frac{-13 \sqrt{15} A(4,0)+26 \sqrt{6} A(4,2)+13 \sqrt{42} A(4,4)-35 \sqrt{15} A(6,0)+85 \sqrt{7} A(6,2)-5 \sqrt{210} A(6,4)-15 \sqrt{385} A(6,6)}{1716} $$ 0 $$ \frac{1716 A(0,0)+91 A(4,0)+182 \sqrt{10} A(4,2)-39 \sqrt{70} A(4,4)-195 A(6,0)+15 \sqrt{105} A(6,2)+75 \sqrt{14} A(6,4)+15 \sqrt{231} A(6,6)}{1716} $$ 0 $
$ f_{y\left(y^2-3z^2\right)} $$ \frac{5 \left(33 \sqrt{42} B(6,1)+11 \sqrt{105} B(6,3)+3 \sqrt{77} B(6,5)\right)}{3432} $$ 0 $$ \frac{1}{3} \sqrt{\frac{2}{5}} B(2,1)+\frac{5 B(4,1)}{11 \sqrt{3}}-\frac{\sqrt{7} \left(104 \sqrt{3} B(4,3)+5 \left(-7 \sqrt{10} B(6,1)+39 B(6,3)+\sqrt{165} B(6,5)\right)\right)}{3432} $$ 0 $$ \frac{572 \sqrt{15} A(2,0)+572 \sqrt{10} A(2,2)-5 \left(13 \sqrt{15} A(4,0)+338 \sqrt{6} A(4,2)+91 \sqrt{42} A(4,4)+35 \sqrt{15} A(6,0)+5 \sqrt{7} A(6,2)-35 \sqrt{210} A(6,4)-15 \sqrt{385} A(6,6)\right)}{17160} $$ 0 $$ \frac{3432 A(0,0)+572 A(2,0)-572 \sqrt{6} A(2,2)+117 A(4,0)-78 \sqrt{10} A(4,2)+39 \sqrt{70} A(4,4)-565 A(6,0)-85 \sqrt{105} A(6,2)-75 \sqrt{14} A(6,4)-5 \sqrt{231} A(6,6)}{3432} $

Rotation matrix used

Rotation matrix used

$ $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ f_{z\left(3y^2-z^2\right)} $$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{\frac{5}{2}}}{2} $$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $
$ f_{\text{xyz}} $$ 0 $$ \frac{i}{\sqrt{2}} $$ 0 $$ 0 $$ 0 $$ -\frac{i}{\sqrt{2}} $$ 0 $
$ f_{z\left(5x^2-r^2\right)} $$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $$ -\frac{\sqrt{\frac{3}{2}}}{2} $$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $
$ f_{x\left(5x^2-3r^2\right)} $$ \frac{\sqrt{5}}{4} $$ 0 $$ -\frac{\sqrt{3}}{4} $$ 0 $$ \frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{5}}{4} $
$ f_{y\left(5x^2-r^2\right)} $$ \frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ \frac{1}{4} i \sqrt{\frac{15}{2}} $
$ f_{x\left(y^2-z^2\right)} $$ -\frac{\sqrt{3}}{4} $$ 0 $$ -\frac{\sqrt{5}}{4} $$ 0 $$ \frac{\sqrt{5}}{4} $$ 0 $$ \frac{\sqrt{3}}{4} $
$ f_{y\left(y^2-3z^2\right)} $$ -\frac{i}{4 \sqrt{2}} $$ 0 $$ -\frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{1}{4} i \sqrt{\frac{15}{2}} $$ 0 $$ -\frac{i}{4 \sqrt{2}} $

Irriducible representations and their onsite energy

Irriducible representations and their onsite energy

$$\frac{3432 A(0,0)+572 A(2,0)-572 \sqrt{6} A(2,2)+117 A(4,0)-78 \sqrt{10} A(4,2)+39 \sqrt{70} A(4,4)+590 A(6,0)+80 \sqrt{105} A(6,2)+90 \sqrt{14} A(6,4)}{3432}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{35}{2 \pi }} \cos (\theta ) \left(6 \sin ^2(\theta ) \cos (2 \phi )+5 \cos (2 \theta )-1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{8} \sqrt{\frac{35}{2 \pi }} z \left(-3 x^2+3 y^2-5 z^2+3\right)$$
$$\frac{1}{429} \left(429 A(0,0)-91 A(4,0)-13 \sqrt{70} A(4,4)+30 A(6,0)-30 \sqrt{14} A(6,4)\right)$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{4} \sqrt{\frac{105}{\pi }} \sin ^2(\theta ) \cos (\theta ) \sin (2 \phi )$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{2} \sqrt{\frac{105}{\pi }} x y z$$
$$A(0,0)+\frac{1}{10} A(2,0)+\frac{572 \sqrt{6} A(2,2)-221 A(4,0)+78 \sqrt{10} A(4,2)+65 \sqrt{70} A(4,4)+450 A(6,0)-80 \sqrt{105} A(6,2)+150 \sqrt{14} A(6,4)}{3432}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{21}{2 \pi }} \cos (\theta ) \left(10 \sin ^2(\theta ) \cos (2 \phi )-5 \cos (2 \theta )+1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{8} \sqrt{\frac{21}{2 \pi }} z \left(5 x^2-5 y^2-5 z^2+3\right)$$
$$\frac{8580 A(0,0)-1144 A(2,0)+1144 \sqrt{6} A(2,2)+585 A(4,0)-390 \sqrt{10} A(4,2)+195 \sqrt{70} A(4,4)-625 A(6,0)+125 \sqrt{105} A(6,2)-375 \sqrt{14} A(6,4)+125 \sqrt{231} A(6,6)}{8580}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{7}{\pi }} \sin (\theta ) \cos (\phi ) \left(10 \sin ^2(\theta ) \cos (2 \phi )-5 \cos (2 \theta )-7\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{7}{\pi }} x \left(5 x^2-15 y^2-15 z^2+3\right)$$
$$\frac{17160 A(0,0)-5148 A(2,0)+572 \sqrt{6} A(2,2)+1495 A(4,0)-650 \sqrt{10} A(4,2)-195 \sqrt{70} A(4,4)-375 A(6,0)+25 \sqrt{105} A(6,2)+375 \sqrt{14} A(6,4)-375 \sqrt{231} A(6,6)}{17160}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{21}{2 \pi }} \sin (\theta ) \sin (\phi ) \left(10 \sin ^2(\theta ) \cos (2 \phi )-5 \cos (2 \theta )+1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{21}{2 \pi }} y \left(15 x^2-5 y^2-5 z^2+1\right)$$
$$\frac{1716 A(0,0)+91 A(4,0)+182 \sqrt{10} A(4,2)-39 \sqrt{70} A(4,4)-195 A(6,0)+15 \sqrt{105} A(6,2)+75 \sqrt{14} A(6,4)+15 \sqrt{231} A(6,6)}{1716}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{105}{\pi }} \sin (\theta ) \cos (\phi ) \left(2 \sin ^2(\theta ) \cos (2 \phi )+3 \cos (2 \theta )+1\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{105}{\pi }} x \left(x^2-3 y^2+5 z^2-1\right)$$
$$\frac{3432 A(0,0)+572 A(2,0)-572 \sqrt{6} A(2,2)+117 A(4,0)-78 \sqrt{10} A(4,2)+39 \sqrt{70} A(4,4)-565 A(6,0)-85 \sqrt{105} A(6,2)-75 \sqrt{14} A(6,4)-5 \sqrt{231} A(6,6)}{3432}$$
$$\psi(\theta,\phi)=\phantom{\sqrt{\frac{1}{1}}}$$ $$-\frac{1}{16} \sqrt{\frac{35}{2 \pi }} \sin (\theta ) \sin (\phi ) \left(2 \sin ^2(\theta ) \cos (2 \phi )+7 \cos (2 \theta )+5\right)$$
$$\psi(\hat{x},\hat{y},\hat{z})=\phantom{\sqrt{\frac{1}{1}}}$$ $$\frac{1}{16} \sqrt{\frac{35}{2 \pi }} y \left(-3 x^2+y^2-15 z^2+3\right)$$

Coupling between two shells

Click on one of the subsections to expand it or

Potential for s-p orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & k\neq 1\lor (m\neq -1\land m\neq 1) \\ \sqrt{\frac{3}{2}} \text{Ma} & k=1\land m=-1 \\ -\sqrt{\frac{3}{2}} \text{Ma} & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, k != 1 || (m != -1 && m != 1)}, {Sqrt[3/2]*Ma, k == 1 && m == -1}}, -(Sqrt[3/2]*Ma)]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{1, 1, (-1)*((sqrt(3/2))*(Ma))} , 
       {1,-1, (sqrt(3/2))*(Ma)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-1}^{(1)}} $ $ {Y_{0}^{(1)}} $ $ {Y_{1}^{(1)}} $
$ {Y_{0}^{(0)}} $$ \frac{\text{Ma}}{\sqrt{2}} $$ 0 $$ -\frac{\text{Ma}}{\sqrt{2}} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ p_z $ $ p_x $ $ p_y $
$ \text{s} $$ 0 $$ \text{Ma} $$ 0 $

Potential for s-d orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & k\neq 2\lor (m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2) \\ A(2,2) & k=2\land (m=-2\lor m=2) \\ i B(2,1) & k=2\land (m=-1\lor m=1) \\ A(2,0) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, k != 2 || (m != -2 && m != -1 && m != 0 && m != 1 && m != 2)}, {A[2, 2], k == 2 && (m == -2 || m == 2)}, {I*B[2, 1], k == 2 && (m == -1 || m == 1)}}, A[2, 0]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{2, 0, A(2,0)} , 
       {2,-1, (I)*(B(2,1))} , 
       {2, 1, (I)*(B(2,1))} , 
       {2,-2, A(2,2)} , 
       {2, 2, A(2,2)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $
$ {Y_{0}^{(0)}} $$ \frac{A(2,2)}{\sqrt{5}} $$ -\frac{i B(2,1)}{\sqrt{5}} $$ \frac{A(2,0)}{\sqrt{5}} $$ -\frac{i B(2,1)}{\sqrt{5}} $$ \frac{A(2,2)}{\sqrt{5}} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ d_{\text{yz}} $ $ d_{\text{xz}} $ $ d_{3x^2-r^2} $ $ d_{\text{xz}} $ $ d_{y^2-z^2} $
$ \text{s} $$ \sqrt{\frac{2}{5}} B(2,1) $$ 0 $$ -\frac{A(2,0)-\sqrt{6} A(2,2)}{2 \sqrt{5}} $$ 0 $$ -\frac{1}{2} \sqrt{\frac{3}{5}} A(2,0)-\frac{A(2,2)}{\sqrt{10}} $

Potential for s-f orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & k\neq 3\lor (m\neq -3\land m\neq -2\land m\neq -1\land m\neq 1\land m\neq 2\land m\neq 3) \\ -A(3,3) & k=3\land m=-3 \\ -i B(3,2) & k=3\land m=-2 \\ -A(3,1) & k=3\land m=-1 \\ A(3,1) & k=3\land m=1 \\ i B(3,2) & k=3\land m=2 \\ A(3,3) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, k != 3 || (m != -3 && m != -2 && m != -1 && m != 1 && m != 2 && m != 3)}, {-A[3, 3], k == 3 && m == -3}, {(-I)*B[3, 2], k == 3 && m == -2}, {-A[3, 1], k == 3 && m == -1}, {A[3, 1], k == 3 && m == 1}, {I*B[3, 2], k == 3 && m == 2}}, A[3, 3]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{3,-1, (-1)*(A(3,1))} , 
       {3, 1, A(3,1)} , 
       {3,-2, (-I)*(B(3,2))} , 
       {3, 2, (I)*(B(3,2))} , 
       {3,-3, (-1)*(A(3,3))} , 
       {3, 3, A(3,3)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ {Y_{0}^{(0)}} $$ -\frac{A(3,3)}{\sqrt{7}} $$ \frac{i B(3,2)}{\sqrt{7}} $$ -\frac{A(3,1)}{\sqrt{7}} $$ 0 $$ \frac{A(3,1)}{\sqrt{7}} $$ -\frac{i B(3,2)}{\sqrt{7}} $$ \frac{A(3,3)}{\sqrt{7}} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ f_{z\left(3y^2-z^2\right)} $ $ f_{\text{xyz}} $ $ f_{z\left(5x^2-r^2\right)} $ $ f_{x\left(5x^2-3r^2\right)} $ $ f_{y\left(5x^2-r^2\right)} $ $ f_{x\left(y^2-z^2\right)} $ $ f_{y\left(y^2-3z^2\right)} $
$ \text{s} $$ 0 $$ -\sqrt{\frac{2}{7}} B(3,2) $$ 0 $$ \frac{1}{14} \left(\sqrt{21} A(3,1)-\sqrt{35} A(3,3)\right) $$ 0 $$ \frac{1}{14} \left(\sqrt{35} A(3,1)+\sqrt{21} A(3,3)\right) $$ 0 $

Potential for p-d orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & (k\neq 3\land (k\neq 1\lor (m\neq -1\land m\neq 1)))\lor (m\neq -3\land m\neq -2\land m\neq -1\land m\neq 1\land m\neq 2\land m\neq 3) \\ -A(1,1) & k=1\land m=-1 \\ A(1,1) & k=1\land m=1 \\ -A(3,3) & k=3\land m=-3 \\ -i B(3,2) & k=3\land m=-2 \\ -A(3,1) & k=3\land m=-1 \\ A(3,1) & k=3\land m=1 \\ i B(3,2) & k=3\land m=2 \\ A(3,3) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, (k != 3 && (k != 1 || (m != -1 && m != 1))) || (m != -3 && m != -2 && m != -1 && m != 1 && m != 2 && m != 3)}, {-A[1, 1], k == 1 && m == -1}, {A[1, 1], k == 1 && m == 1}, {-A[3, 3], k == 3 && m == -3}, {(-I)*B[3, 2], k == 3 && m == -2}, {-A[3, 1], k == 3 && m == -1}, {A[3, 1], k == 3 && m == 1}, {I*B[3, 2], k == 3 && m == 2}}, A[3, 3]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{1,-1, (-1)*(A(1,1))} , 
       {1, 1, A(1,1)} , 
       {3,-1, (-1)*(A(3,1))} , 
       {3, 1, A(3,1)} , 
       {3,-2, (-I)*(B(3,2))} , 
       {3, 2, (I)*(B(3,2))} , 
       {3,-3, (-1)*(A(3,3))} , 
       {3, 3, A(3,3)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-2}^{(2)}} $ $ {Y_{-1}^{(2)}} $ $ {Y_{0}^{(2)}} $ $ {Y_{1}^{(2)}} $ $ {Y_{2}^{(2)}} $
$ {Y_{-1}^{(1)}} $$ \frac{1}{35} \left(\sqrt{15} A(3,1)-7 \sqrt{10} A(1,1)\right) $$ 0 $$ \frac{A(1,1)}{\sqrt{15}}-\frac{3}{7} \sqrt{\frac{2}{5}} A(3,1) $$ \frac{1}{7} i \sqrt{6} B(3,2) $$ -\frac{3}{7} A(3,3) $
$ {Y_{0}^{(1)}} $$ \frac{1}{7} i \sqrt{3} B(3,2) $$ -\frac{7 A(1,1)+2 \sqrt{6} A(3,1)}{7 \sqrt{5}} $$ 0 $$ \frac{A(1,1)}{\sqrt{5}}+\frac{2}{7} \sqrt{\frac{6}{5}} A(3,1) $$ -\frac{1}{7} i \sqrt{3} B(3,2) $
$ {Y_{1}^{(1)}} $$ \frac{3}{7} A(3,3) $$ -\frac{1}{7} i \sqrt{6} B(3,2) $$ \frac{3}{7} \sqrt{\frac{2}{5}} A(3,1)-\frac{A(1,1)}{\sqrt{15}} $$ 0 $$ \sqrt{\frac{2}{5}} A(1,1)-\frac{1}{7} \sqrt{\frac{3}{5}} A(3,1) $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ d_{\text{yz}} $ $ d_{\text{xz}} $ $ d_{3x^2-r^2} $ $ d_{\text{xz}} $ $ d_{y^2-z^2} $
$ p_z $$ 0 $$ -\sqrt{\frac{2}{5}} A(1,1)-\frac{4}{7} \sqrt{\frac{3}{5}} A(3,1) $$ 0 $$ -\frac{1}{7} \sqrt{6} B(3,2) $$ 0 $
$ p_x $$ -\frac{1}{7} \sqrt{6} B(3,2) $$ 0 $$ \frac{1}{210} \left(-28 \sqrt{30} A(1,1)+27 \sqrt{5} A(3,1)-45 \sqrt{3} A(3,3)\right) $$ 0 $$ \frac{1}{14} \left(\sqrt{15} A(3,1)+3 A(3,3)\right) $
$ p_y $$ 0 $$ -\frac{1}{7} \sqrt{6} B(3,2) $$ 0 $$ \frac{1}{35} \left(-7 \sqrt{10} A(1,1)+\sqrt{15} A(3,1)+15 A(3,3)\right) $$ 0 $

Potential for p-f orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & (k\neq 2\land k\neq 4)\lor (k\neq 4\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2)\lor (m\neq -4\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 0\land m\neq 1\land m\neq 2\land m\neq 3\land m\neq 4) \\ A(2,2) & k=2\land (m=-2\lor m=2) \\ i B(2,1) & k=2\land (m=-1\lor m=1) \\ A(2,0) & k=2\land m=0 \\ A(4,4) & k=4\land (m=-4\lor m=4) \\ i B(4,3) & k=4\land (m=-3\lor m=3) \\ A(4,2) & k=4\land (m=-2\lor m=2) \\ i B(4,1) & k=4\land (m=-1\lor m=1) \\ A(4,0) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, (k != 2 && k != 4) || (k != 4 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2) || (m != -4 && m != -3 && m != -2 && m != -1 && m != 0 && m != 1 && m != 2 && m != 3 && m != 4)}, {A[2, 2], k == 2 && (m == -2 || m == 2)}, {I*B[2, 1], k == 2 && (m == -1 || m == 1)}, {A[2, 0], k == 2 && m == 0}, {A[4, 4], k == 4 && (m == -4 || m == 4)}, {I*B[4, 3], k == 4 && (m == -3 || m == 3)}, {A[4, 2], k == 4 && (m == -2 || m == 2)}, {I*B[4, 1], k == 4 && (m == -1 || m == 1)}}, A[4, 0]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{2, 0, A(2,0)} , 
       {2,-1, (I)*(B(2,1))} , 
       {2, 1, (I)*(B(2,1))} , 
       {2,-2, A(2,2)} , 
       {2, 2, A(2,2)} , 
       {4, 0, A(4,0)} , 
       {4,-1, (I)*(B(4,1))} , 
       {4, 1, (I)*(B(4,1))} , 
       {4,-2, A(4,2)} , 
       {4, 2, A(4,2)} , 
       {4,-3, (I)*(B(4,3))} , 
       {4, 3, (I)*(B(4,3))} , 
       {4,-4, A(4,4)} , 
       {4, 4, A(4,4)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ {Y_{-1}^{(1)}} $$ \frac{3 A(2,2)}{\sqrt{35}}-\frac{A(4,2)}{3 \sqrt{21}} $$ -\frac{i \left(3 \sqrt{30} B(2,1)-5 B(4,1)\right)}{15 \sqrt{7}} $$ \frac{1}{15} \sqrt{\frac{2}{7}} (9 A(2,0)-5 A(4,0)) $$ -\frac{i \left(27 B(2,1)-5 \sqrt{30} B(4,1)\right)}{45 \sqrt{7}} $$ \frac{1}{105} \left(3 \sqrt{21} A(2,2)-5 \sqrt{35} A(4,2)\right) $$ \frac{1}{3} i B(4,3) $$ -\frac{2 A(4,4)}{3 \sqrt{3}} $
$ {Y_{0}^{(1)}} $$ -\frac{i B(4,3)}{3 \sqrt{3}} $$ \sqrt{\frac{3}{35}} A(2,2)+\frac{2 A(4,2)}{3 \sqrt{7}} $$ -\frac{1}{105} i \left(6 \sqrt{42} B(2,1)+5 \sqrt{35} B(4,1)\right) $$ \frac{27 A(2,0)+20 A(4,0)}{15 \sqrt{21}} $$ -\frac{1}{105} i \left(6 \sqrt{42} B(2,1)+5 \sqrt{35} B(4,1)\right) $$ \sqrt{\frac{3}{35}} A(2,2)+\frac{2 A(4,2)}{3 \sqrt{7}} $$ -\frac{i B(4,3)}{3 \sqrt{3}} $
$ {Y_{1}^{(1)}} $$ -\frac{2 A(4,4)}{3 \sqrt{3}} $$ \frac{1}{3} i B(4,3) $$ \frac{1}{105} \left(3 \sqrt{21} A(2,2)-5 \sqrt{35} A(4,2)\right) $$ -\frac{i \left(27 B(2,1)-5 \sqrt{30} B(4,1)\right)}{45 \sqrt{7}} $$ \frac{1}{15} \sqrt{\frac{2}{7}} (9 A(2,0)-5 A(4,0)) $$ -\frac{i \left(3 \sqrt{30} B(2,1)-5 B(4,1)\right)}{15 \sqrt{7}} $$ \frac{3 A(2,2)}{\sqrt{35}}-\frac{A(4,2)}{3 \sqrt{21}} $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ f_{z\left(3y^2-z^2\right)} $ $ f_{\text{xyz}} $ $ f_{z\left(5x^2-r^2\right)} $ $ f_{x\left(5x^2-3r^2\right)} $ $ f_{y\left(5x^2-r^2\right)} $ $ f_{x\left(y^2-z^2\right)} $ $ f_{y\left(y^2-3z^2\right)} $
$ p_z $$ -\frac{27 \sqrt{10} A(2,0)+18 \sqrt{15} A(2,2)+20 \sqrt{10} A(4,0)+60 A(4,2)}{60 \sqrt{21}} $$ 0 $$ \frac{1}{420} \left(-27 \sqrt{14} A(2,0)+30 \sqrt{21} A(2,2)-20 \sqrt{14} A(4,0)+20 \sqrt{35} A(4,2)\right) $$ 0 $$ \frac{1}{420} \left(-12 \sqrt{21} B(2,1)-5 \sqrt{70} B(4,1)+35 \sqrt{10} B(4,3)\right) $$ 0 $$ -\frac{3 B(2,1)}{\sqrt{35}}-\frac{15 \sqrt{7} B(4,1)+7 B(4,3)}{42 \sqrt{6}} $
$ p_x $$ 0 $$ \sqrt{\frac{6}{35}} B(2,1)-\frac{B(4,1)}{3 \sqrt{7}}+\frac{1}{3} B(4,3) $$ 0 $$ \frac{1}{630} \left(-27 \sqrt{21} A(2,0)+81 \sqrt{14} A(2,2)+5 \left(3 \sqrt{21} A(4,0)-2 \sqrt{210} A(4,2)+7 \sqrt{30} A(4,4)\right)\right) $$ 0 $$ \frac{1}{210} \left(-9 \sqrt{35} A(2,0)-3 \sqrt{210} A(2,2)+5 \left(\sqrt{35} A(4,0)-2 \sqrt{14} A(4,2)-7 \sqrt{2} A(4,4)\right)\right) $$ 0 $
$ p_y $$ \frac{3 B(2,1)}{\sqrt{35}}-\frac{13 \sqrt{7} B(4,1)+21 B(4,3)}{42 \sqrt{6}} $$ 0 $$ \frac{1}{420} \left(-12 \sqrt{21} B(2,1)-5 \sqrt{70} B(4,1)+35 \sqrt{10} B(4,3)\right) $$ 0 $$ \frac{1}{420} \left(-9 \sqrt{14} A(2,0)+42 \sqrt{21} A(2,2)+5 \sqrt{14} A(4,0)-70 \sqrt{5} A(4,4)\right) $$ 0 $$ \frac{-27 \sqrt{210} A(2,0)-54 \sqrt{35} A(2,2)+5 \sqrt{3} \left(3 \sqrt{70} A(4,0)+16 \sqrt{7} A(4,2)+14 A(4,4)\right)}{1260} $

Potential for d-f orbital mixing

Potential parameterized with onsite energies of irriducible representations

Potential parameterized with onsite energies of irriducible representations

$$A_{k,m} = \begin{cases} 0 & (k\neq 1\land k\neq 3\land k\neq 5)\lor (k\neq 3\land k\neq 5\land m\neq -1\land m\neq 1)\lor (k\neq 5\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 1\land m\neq 2\land m\neq 3)\lor (m\neq -5\land m\neq -4\land m\neq -3\land m\neq -2\land m\neq -1\land m\neq 1\land m\neq 2\land m\neq 3\land m\neq 4\land m\neq 5) \\ -A(1,1) & k=1\land m=-1 \\ A(1,1) & k=1\land m=1 \\ -A(3,3) & k=3\land m=-3 \\ -i B(3,2) & k=3\land m=-2 \\ -A(3,1) & k=3\land m=-1 \\ A(3,1) & k=3\land m=1 \\ i B(3,2) & k=3\land m=2 \\ A(3,3) & k=3\land m=3 \\ -A(5,5) & k=5\land m=-5 \\ -i B(5,4) & k=5\land m=-4 \\ -A(5,3) & k=5\land m=-3 \\ -i B(5,2) & k=5\land m=-2 \\ -A(5,1) & k=5\land m=-1 \\ A(5,1) & k=5\land m=1 \\ i B(5,2) & k=5\land m=2 \\ A(5,3) & k=5\land m=3 \\ i B(5,4) & k=5\land m=4 \\ A(5,5) & \text{True} \end{cases}$$

Input format suitable for Mathematica (Quanty.nb)

Input format suitable for Mathematica (Quanty.nb)

Akm_C2_X.Quanty.nb
Akm[k_,m_]:=Piecewise[{{0, (k != 1 && k != 3 && k != 5) || (k != 3 && k != 5 && m != -1 && m != 1) || (k != 5 && m != -3 && m != -2 && m != -1 && m != 1 && m != 2 && m != 3) || (m != -5 && m != -4 && m != -3 && m != -2 && m != -1 && m != 1 && m != 2 && m != 3 && m != 4 && m != 5)}, {-A[1, 1], k == 1 && m == -1}, {A[1, 1], k == 1 && m == 1}, {-A[3, 3], k == 3 && m == -3}, {(-I)*B[3, 2], k == 3 && m == -2}, {-A[3, 1], k == 3 && m == -1}, {A[3, 1], k == 3 && m == 1}, {I*B[3, 2], k == 3 && m == 2}, {A[3, 3], k == 3 && m == 3}, {-A[5, 5], k == 5 && m == -5}, {(-I)*B[5, 4], k == 5 && m == -4}, {-A[5, 3], k == 5 && m == -3}, {(-I)*B[5, 2], k == 5 && m == -2}, {-A[5, 1], k == 5 && m == -1}, {A[5, 1], k == 5 && m == 1}, {I*B[5, 2], k == 5 && m == 2}, {A[5, 3], k == 5 && m == 3}, {I*B[5, 4], k == 5 && m == 4}}, A[5, 5]]

Input format suitable for Quanty

Input format suitable for Quanty

Akm_C2_X.Quanty
Akm = {{1,-1, (-1)*(A(1,1))} , 
       {1, 1, A(1,1)} , 
       {3,-1, (-1)*(A(3,1))} , 
       {3, 1, A(3,1)} , 
       {3,-2, (-I)*(B(3,2))} , 
       {3, 2, (I)*(B(3,2))} , 
       {3,-3, (-1)*(A(3,3))} , 
       {3, 3, A(3,3)} , 
       {5,-1, (-1)*(A(5,1))} , 
       {5, 1, A(5,1)} , 
       {5,-2, (-I)*(B(5,2))} , 
       {5, 2, (I)*(B(5,2))} , 
       {5,-3, (-1)*(A(5,3))} , 
       {5, 3, A(5,3)} , 
       {5,-4, (-I)*(B(5,4))} , 
       {5, 4, (I)*(B(5,4))} , 
       {5,-5, (-1)*(A(5,5))} , 
       {5, 5, A(5,5)} }

The Hamiltonian on a basis of spherical Harmonics

The Hamiltonian on a basis of spherical Harmonics

$ $ $ {Y_{-3}^{(3)}} $ $ {Y_{-2}^{(3)}} $ $ {Y_{-1}^{(3)}} $ $ {Y_{0}^{(3)}} $ $ {Y_{1}^{(3)}} $ $ {Y_{2}^{(3)}} $ $ {Y_{3}^{(3)}} $
$ {Y_{-2}^{(2)}} $$ \frac{1}{231} \left(-33 \sqrt{21} A(1,1)+11 \sqrt{14} A(3,1)-\sqrt{35} A(5,1)\right) $$ 0 $$ \frac{A(1,1)}{\sqrt{35}}-2 \sqrt{\frac{2}{105}} A(3,1)+\frac{5 A(5,1)}{11 \sqrt{21}} $$ \frac{1}{231} i \left(22 \sqrt{7} B(3,2)-35 B(5,2)\right) $$ \frac{5}{33} \sqrt{2} A(5,3)-\frac{1}{3} \sqrt{\frac{2}{7}} A(3,3) $$ -\frac{1}{11} i \sqrt{10} B(5,4) $$ \frac{5}{11} \sqrt{\frac{2}{3}} A(5,5) $
$ {Y_{-1}^{(2)}} $$ \frac{1}{231} i \sqrt{5} \left(11 \sqrt{7} B(3,2)-7 B(5,2)\right) $$ -\sqrt{\frac{2}{7}} A(1,1)-\frac{A(3,1)}{\sqrt{21}}+\frac{2}{11} \sqrt{\frac{10}{21}} A(5,1) $$ 0 $$ \sqrt{\frac{3}{35}} A(1,1)-\frac{1}{3} \sqrt{\frac{2}{35}} A(3,1)-\frac{20 A(5,1)}{33 \sqrt{7}} $$ \frac{i \left(11 \sqrt{7} B(3,2)+35 B(5,2)\right)}{77 \sqrt{3}} $$ -\frac{1}{231} \sqrt{5} \left(11 \sqrt{7} A(3,3)+28 A(5,3)\right) $$ \frac{2}{11} i \sqrt{\frac{5}{3}} B(5,4) $
$ {Y_{0}^{(2)}} $$ \frac{1}{3} \sqrt{\frac{5}{7}} A(3,3)-\frac{2}{33} \sqrt{5} A(5,3) $$ \frac{1}{11} i \sqrt{5} B(5,2) $$ -\sqrt{\frac{6}{35}} A(1,1)-\frac{A(3,1)}{\sqrt{35}}-\frac{5}{11} \sqrt{\frac{2}{7}} A(5,1) $$ 0 $$ \sqrt{\frac{6}{35}} A(1,1)+\frac{A(3,1)}{\sqrt{35}}+\frac{5}{11} \sqrt{\frac{2}{7}} A(5,1) $$ -\frac{1}{11} i \sqrt{5} B(5,2) $$ \frac{2}{33} \sqrt{5} A(5,3)-\frac{1}{3} \sqrt{\frac{5}{7}} A(3,3) $
$ {Y_{1}^{(2)}} $$ -\frac{2}{11} i \sqrt{\frac{5}{3}} B(5,4) $$ \frac{1}{3} \sqrt{\frac{5}{7}} A(3,3)+\frac{4}{33} \sqrt{5} A(5,3) $$ -\frac{i \left(11 \sqrt{7} B(3,2)+35 B(5,2)\right)}{77 \sqrt{3}} $$ -\sqrt{\frac{3}{35}} A(1,1)+\frac{1}{3} \sqrt{\frac{2}{35}} A(3,1)+\frac{20 A(5,1)}{33 \sqrt{7}} $$ 0 $$ \sqrt{\frac{2}{7}} A(1,1)+\frac{A(3,1)}{\sqrt{21}}-\frac{2}{11} \sqrt{\frac{10}{21}} A(5,1) $$ -\frac{1}{231} i \sqrt{5} \left(11 \sqrt{7} B(3,2)-7 B(5,2)\right) $
$ {Y_{2}^{(2)}} $$ -\frac{5}{11} \sqrt{\frac{2}{3}} A(5,5) $$ \frac{1}{11} i \sqrt{10} B(5,4) $$ \frac{1}{3} \sqrt{\frac{2}{7}} A(3,3)-\frac{5}{33} \sqrt{2} A(5,3) $$ \frac{5}{33} i B(5,2)-\frac{2 i B(3,2)}{3 \sqrt{7}} $$ -\frac{A(1,1)}{\sqrt{35}}+2 \sqrt{\frac{2}{105}} A(3,1)-\frac{5 A(5,1)}{11 \sqrt{21}} $$ 0 $$ \frac{1}{231} \left(33 \sqrt{21} A(1,1)-11 \sqrt{14} A(3,1)+\sqrt{35} A(5,1)\right) $

The Hamiltonian on a basis of symmetric functions

The Hamiltonian on a basis of symmetric functions

$ $ $ f_{z\left(3y^2-z^2\right)} $ $ f_{\text{xyz}} $ $ f_{z\left(5x^2-r^2\right)} $ $ f_{x\left(5x^2-3r^2\right)} $ $ f_{y\left(5x^2-r^2\right)} $ $ f_{x\left(y^2-z^2\right)} $ $ f_{y\left(y^2-3z^2\right)} $
$ d_{\text{yz}} $$ 0 $$ -\sqrt{\frac{2}{7}} A(1,1)-\frac{A(3,1)}{\sqrt{21}}+\frac{1}{231} \sqrt{5} \left(11 \sqrt{7} A(3,3)+2 \sqrt{42} A(5,1)+28 A(5,3)\right) $$ 0 $$ \frac{2}{3} \sqrt{\frac{2}{7}} B(3,2)+\frac{5 \left(B(5,2)-\sqrt{3} B(5,4)\right)}{33 \sqrt{2}} $$ 0 $$ \frac{1}{11} \sqrt{\frac{5}{6}} \left(3 B(5,2)+\sqrt{3} B(5,4)\right) $$ 0 $
$ d_{\text{xz}} $$ \frac{1}{924} \left(55 \sqrt{14} A(3,1)+11 \sqrt{210} A(3,3)+28 \left(\sqrt{35} A(5,1)+\sqrt{30} A(5,3)\right)\right) $$ 0 $$ -\frac{4 A(1,1)}{\sqrt{35}}-\frac{1}{2} \sqrt{\frac{3}{70}} A(3,1)+\frac{5 \left(-11 \sqrt{7} A(3,3)+6 \sqrt{42} A(5,1)-28 A(5,3)\right)}{462 \sqrt{2}} $$ 0 $$ \frac{5}{66} \left(\sqrt{3} B(5,2)-3 B(5,4)\right)-\frac{B(3,2)}{\sqrt{21}} $$ 0 $$ \frac{1}{462} \sqrt{5} \left(22 \sqrt{7} B(3,2)+49 B(5,2)+7 \sqrt{3} B(5,4)\right) $
$ d_{3x^2-r^2} $$ 0 $$ \frac{1}{11} \sqrt{\frac{5}{2}} \left(B(5,2)-\sqrt{3} B(5,4)\right) $$ 0 $$ -3 \sqrt{\frac{2}{35}} A(1,1)+\frac{2 A(3,1)}{\sqrt{105}}+\frac{1}{924} \left(-88 \sqrt{7} A(3,3)-25 \sqrt{42} A(5,1)+175 A(5,3)-105 \sqrt{5} A(5,5)\right) $$ 0 $$ \frac{1}{44} \left(-\sqrt{70} A(5,1)+\sqrt{15} A(5,3)+5 \sqrt{3} A(5,5)\right) $$ 0 $
$ d_{\text{xz}} $$ \frac{1}{462} \sqrt{5} \left(-22 \sqrt{7} B(3,2)+35 B(5,2)+21 \sqrt{3} B(5,4)\right) $$ 0 $$ \frac{5}{66} \left(\sqrt{3} B(5,2)-3 B(5,4)\right)-\frac{B(3,2)}{\sqrt{21}} $$ 0 $$ \frac{-264 \sqrt{70} A(1,1)+77 \sqrt{105} A(3,1)+55 \sqrt{7} A(3,3)-25 \sqrt{42} A(5,1)-175 A(5,3)+525 \sqrt{5} A(5,5)}{2310 \sqrt{2}} $$ 0 $$ \frac{55 \sqrt{7} A(3,1)+11 \sqrt{105} A(3,3)-7 \left(\sqrt{70} A(5,1)+5 \sqrt{3} \left(\sqrt{5} A(5,3)+A(5,5)\right)\right)}{462 \sqrt{2}} $
$ d_{y^2-z^2} $$ 0 $$ \frac{1}{11} \sqrt{\frac{5}{2}} \left(\sqrt{3} B(5,2)+B(5,4)\right) $$ 0 $$ -\frac{1}{3} \sqrt{\frac{5}{7}} A(3,1)-\frac{A(3,3)}{\sqrt{21}}+\frac{5}{132} \left(\sqrt{3} \left(A(5,3)+\sqrt{5} A(5,5)\right)-\sqrt{14} A(5,1)\right) $$ 0 $$ \frac{1}{924} \left(-132 \sqrt{14} A(1,1)-44 \sqrt{21} A(3,1)+44 \sqrt{35} A(3,3)-13 \sqrt{210} A(5,1)-77 \sqrt{5} A(5,3)-105 A(5,5)\right) $$ 0 $

Table of several point groups

Return to Main page on Point Groups

Nonaxial groups C1 Cs Ci
Cn groups C2 C3 C4 C5 C6 C7 C8
Dn groups D2 D3 D4 D5 D6 D7 D8
Cnv groups C2v C3v C4v C5v C6v C7v C8v
Cnh groups C2h C3h C4h C5h C6h
Dnh groups D2h D3h D4h D5h D6h D7h D8h
Dnd groups D2d D3d D4d D5d D6d D7d D8d
Sn groups S2 S4 S6 S8 S10 S12
Cubic groups T Th Td O Oh I Ih
Linear groups C$\infty$v D$\infty$h

You are here: Quanty - a quantum many body script language » Physics, Chemistry and Mathematics » Point groups » Point Group C2 » Orientation X

Print/export